Ngā Whāinga Ako ^🔗

Explain the basic structure and wavelength of a standing wave

Standing Waves ^🔗

Most musical instruments produce sound through vibration of standing waves in strings or columns of air.

Recall: Waves in a String ^🔗

1. The particles oscillate perpendicular to the direction of the wave,
2. the wave appears to move along the string,
3. the wave is reflected and can travel back and forth.

• When the wave reflects at the fixed point, it is inverted and will interfere with other waves.
• Peaks and troughs are points of maximum potential energy, and the line of equilibrium is a point of maximum kinetic energy.
• Most waves that interfere this way will having moving nodes and antinodes (non-standing waves).

Producing Standing Waves ^🔗

• For a string that is fixed at both ends, only waves with the correct wavelength to put a node at each end will form a standing wave.
• Waves that do not ‘fit’ will not form a standing wave.

^🔗

Standing Waves ^🔗

• The length of the oscillator is defined as $L$
• The frequency with the longest wavelength that fits into the string/pipe is called the fundamental resonant frequency or 1st harmonic
• On a string, resonant wavelengths are given by $\lambda = \frac{2L}{n}$ where $n$ is the number resonant frequency.

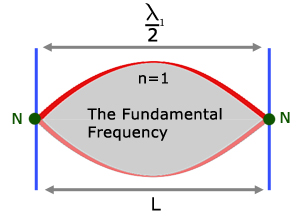
Impact of $L$ on $f$ ^🔗

• Using $\lambda = \frac{2L}{n}$ for a string, we can see the longer the oscillator, the longer the fundamental wavelength.
• Then using $f = \frac{v}{\lambda}$ we can see that this leads to a lower fundamental frequency (lower pitch).

Pātai Tahi ^🔗

A string has length $0.25m$ and speed of sound $330ms^{-1}$.

1. Draw a diagram of the fundamental resonant frequency
2. Calculate the fundamental wavelength
3. Calculate the fundamental frequency
   
   
4. Draw a diagram of the 3rd resonant frequency
5. Calculate the 3rd harmonic wavelength
6. Calculate the 3rd harmonic frequency

Whakatika Tahi ^🔗

1st Harmonic (Fundamental) Frequency:

$$ \begin{aligned} \lambda_{1} &= \frac{2L}{n} = \frac{2 \times 0.25}{1} = 0.5m \newline f_{1} &= \frac{v}{\lambda_{1}} \newline f_{1} &= \frac{330}{0.5} = 660Hz \end{aligned} $$

Whakatika Rua ^🔗

3rd Harmonic Frequency:

$$ \begin{aligned} \lambda_{3} &= \frac{2L}{n} = \frac{2 \times 0.25}{3} = 0.167m \newline f_{3} &= \frac{v}{\lambda_{3}} \newline f_{3} &= \frac{330}{0.167} = 1976Hz \end{aligned} $$

Mahi Tuatahi ^🔗

Head up your book with the date.

Quinn strums a ukulele string such that is oscillates at the 3rd harmonic. The string has a length of $30cm$ and the speed of sound is $343ms^{-1}$.

1. Draw a diagram of the harmonic on the string. Label the nodes and antinodes.
2. What overtone is this?
3. Calculate the wavelength of the harmonic
4. Calculate the frequency of the note emitted
5. Give a reason why the same frequency note played on a trumpet would sound different (with regards to harmonics)

Timbre ^🔗

• An instrument will vibrate at multiple different resonant frequencies (overtones), but the loudest frequency is the note that is heard.
• Different instruments playing the same note will produce a different set of harmonics (overtones), causing the quality of the note to be quite different.

Ngā Whāinga Ako ^🔗

1. Calculate the harmonic frequencies of a string, closed pipe, and open pipe in a variety of situations

Write the date and ngā whāinga ako in your book

^🔗

Mahi Tuatahi ^🔗

Quizziz: https://quizizz.com/admin/quiz/5a7d8747b69214001faec0e9/standing-waves

Musical Wind Instruments ^🔗

• In order to produce different frequencies in a wind instrument, wind is generally sent past a sharp lip.
• Air moving past this sharp lip will create a large number of frequencies, but only specific ones will produce standing waves and therefore resonant frequencies.

Mahi Kāinga Booklet Q13 ^🔗

See One, Do One, Teach One ^🔗

• This method is also known as I do, we do, you do and it is a good way to guide students through a new skill.
• It gets used everywhere from primary school, to Physics class and to doctors in operating theaters.

Step 1: See One ^🔗

• Some police forces have used whistles that have two chambers of different lengths.
• On the above diagram, draw the fundamental standing wave in the shorter chamber, AND label any displacement nodes and antinodes. The fundamental frequencies for the two chambers are 2136 Hz and 1904 Hz. The speed of sound in air is 343 m s–1.
• Calculate the length of the longer chamber.
• Explain how a standing wave is produced in a pipe that is closed at one end.

Step 2: Do One ^🔗

• You have been put into either Group A or Group B - the groups have different questions.
• Your task is to complete your question, using your notes to help you write a good answer.
• Once done, go and check the answers around the room. Use this information to help improve your answer!

You have seen how to do a question and are now doing some vital practice to become an expert.

Step 3: Teach One ^🔗

• In this task, you are now the expert and will be letting someone else See One
• Find someone who is the opposite group to you and use your second blank question to show your partner how to do the question.
• In return, that person can demonstrate how to do their question, to you.

The act of explaining the question in detail to someone else will help you better understand and retain how to do it!

Mahi ^🔗

• Now:
  • Textbook Activity 5A Q5-6
• Mahi Kāinga / Homework:
  • Standing Waves Q11 from the Homework Booklet due on Monday.
  • This must be completed and marked in your exercise book.