Doppler Source

Mahi Tuatahi

P3.3 Worksheet #4 Q2a, b

Doppler Skill 2: Finding \(v_{s}\)

This is relatively straightforward when \(f\) and \(f'\) are known. It becomes more challenging when you do not have both of these variables – we will address this later.

\[ \begin{aligned} & f' = f\frac{v_{w}}{v_{w} \pm v_{s}} \end{aligned} \]

1. Identify when you are in a \(+\) or a \(-\) situtation,
2. Substitute your knowns,
3. Simplify and re-arrange to solve.

Pātai: The Airport

Cameron is watching a plane by the airport. Its engines emit sound at \(2000Hz\); the speed of sound in air is \(330ms^{-1}\).

1. He hears a frequency of \(2500Hz\) as it approaches him. What is the velocity of the plane?
2. He hears a frequency of \(1250Hz\) as it has passed him. What is the velocity of the plane?

Pātai: Doppler Ultrasound

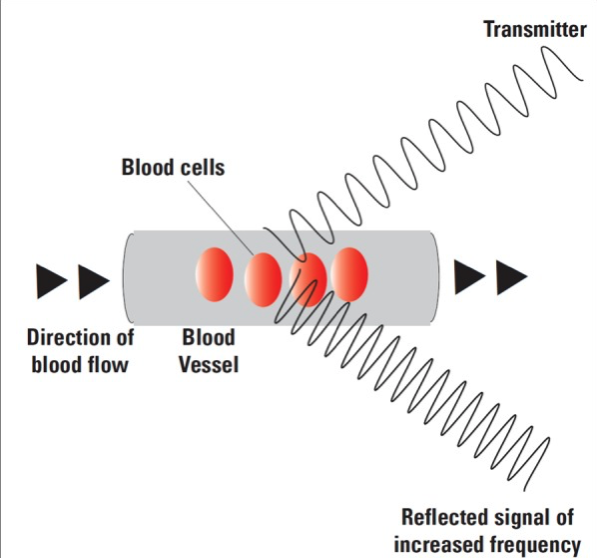
• A Doppler ultrasound is used to measure the flow of blood in blood vessels. This can be used to help find blood clots or constricted vessels. The ultrasound operates at \(4MHz\) and the speed of sound in flesh/blood is around \(1500ms^{-1}\).
• If the return frequency is \(4,005,073.09Hz\), calculate the velocity of the blood towards the device.

Fast Finishers: P3.3 Worksheet #4 Q1a, b