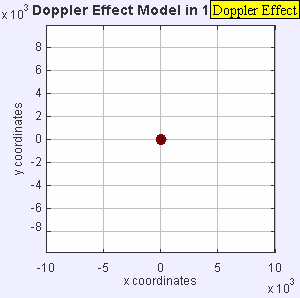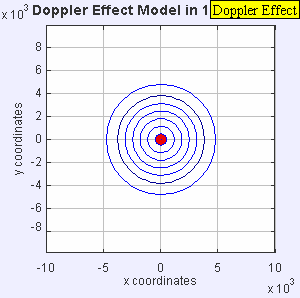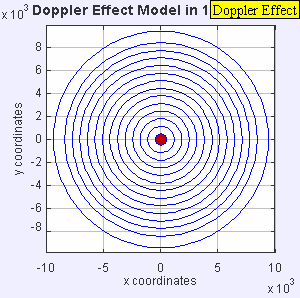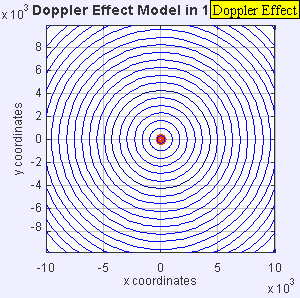
Doppler Equation

Doppler Equation

\[ \begin{aligned} & f' = f\frac{v_{w}}{v_{w} \pm v_{s}} \end{aligned} \]

• \(v_{w}\): the velocity of the wave in the medium (\(ms^{-1}\))
• \(v_{s}\): the velocity of the source (\(ms^{-1}\))
• \(f\): the actual emitted frequency of the wave produced by the source (\(Hz\))
• \(f'\): the observed frequency of the wave (\(Hz\))

Pātai: What is the \(\pm\) symbol?

• Literally: plus OR minus
• In words: \(v_{w} \pm v_{s}\) means the velocity of the wave relative to the source
• Approaching: \(f' = f\frac{v_{w}}{v_{w} - v_{s}}\) because the wave and source are moving in the same direction, the wave appears to be moving slower relative to the source
  • Wavefront is compressed, wavelength is shorter, frequency is higher, pitch is higher
• Receding: \(f' = f\frac{v_{w}}{v_{w} + v_{s}}\) because the wave and source are moving in opposite directions, the wave appears to be moving faster relative to the source
  • Wavefront is expanded, wavelength is longer, frequency is less, pitch is lower

Doppler Skill 1: Calculating \(f'\)

• Activity 6A Q1, Q2

Breaking the Sound Barrier