Ngā Whāinga Ako ^🔗

• Explain the interference of two wave patterns in terms of nodes, anti-nodes and path difference

Diffraction ^🔗

• When waves pass through an opening or bump against a barrier, they will diffract
• Openings: The most diffraction occurs when the opening width and wavelength are similar

^🔗

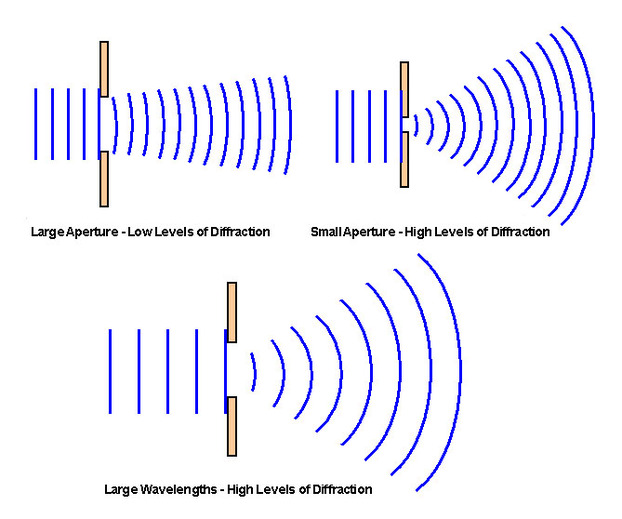
• Barriers: Longer wavelengths diffract best around barriers e.g. AM radio has a longer wavelength than FM and can be better heard in the mountains
• Notice that the wavelength does not change when diffraction occurs.

Constructive vs Destructive Interference ^🔗

• Recall the following:
  • In phase waves constructively interfere
  • Out of phase (180deg) waves destructively interfere
  • Waves not exactly (180deg) out of phase partially interfere

Two Point Source Interference ^🔗

• Two point sources with the same frequency and amplitude are placed near each other
• Their waves will interfere to create points of zero amplitude, and points of 2x amplitude of the original wave

Interference of Light ^🔗

• For light to interfere we need:
  • Waves of the same frequency
  • Waves with the same amplitude
  • Waves with a stable phase relationship (coherent)

• This is usually achieved by passing light from a single source through two very narrow and close slits.

Path Difference ^🔗

• Moving away from the centre point, the distance each travels becomes unequal
• This means the waves will not keep a constant phase relationship
• We call the difference in the distances that they travel the path difference

Worksheet ^🔗

• Collect a worksheet
• Fill out the table by counting the number of wavelengths to each point
• Use the table to determine the path difference for each of the anti-nodal lines
• Highlight the statements in the two boxes on the second page
• Finish the rest of the questions on the sheet

Calculating Path Difference ^🔗

• Path difference can be written as $pd$
• Antinodal Lines: $pd = n\lambda$
• Nodal Lines: $pd = (n - \frac{1}{2})\lambda$

Mahi Tuatahi ^🔗

• If you used the equations, verify by counting wavelengths on the diagram.
• If you used the diagram, verify your answer by doing calculations.

Interference Formula ^🔗

What does it tell us? ^🔗

$$ \begin{aligned} pd &= \frac{dx}{L} \newline \text{Rearranging for x and substiting $pd = n\lambda$:} \newline x &= \frac{n\lambda L}{d} \end{aligned} $$

• as wavelength ($\lambda$) increases, so does the fringe spacing (x)
• as screen distance (L) increases, so does the fringe spacing (x)
• as slit separation (d) increases, the fringe spacing decreases

Interference Formula ^🔗

All this futzing leaves us with a series of formula:

$$ \begin{aligned} pd &= n\lambda \text{ antinodes} \newline pd &= (n- \frac{1}{2})\lambda \text{ nodes} \newline pd &= \frac{dx}{L} \newline \text{OR} \newline pd &= dsin(\theta) \newline &\text{ ^ assumes } \theta \approx \theta ' \end{aligned} $$

Practice ^🔗

• Take some time to try the questions from Textbook Activity 4B
• Check your answers or find some help from the answers on Classroom