Recall: Diffraction 🔗

- Light diffracts just like sound or matter waves
- The longer the wavelength, the greater the diffraction
- Therefore, red diffracts the most, and blue/purple, the least.
Double-Slit vs. Diffraction Gratings 🔗
- A double slit has only two openings, while a diffraction grating has thousands of equally spaced openings!
- This increases the amount of interference that is occurring, which makes the fringes narrower
- This is because there is more interference occurring which results more areas of destructive interference.
Comparing 🔗
Here is a double-slit interference pattern.

Here is a diffraction grating interference pattern.
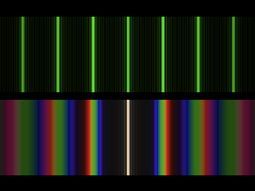
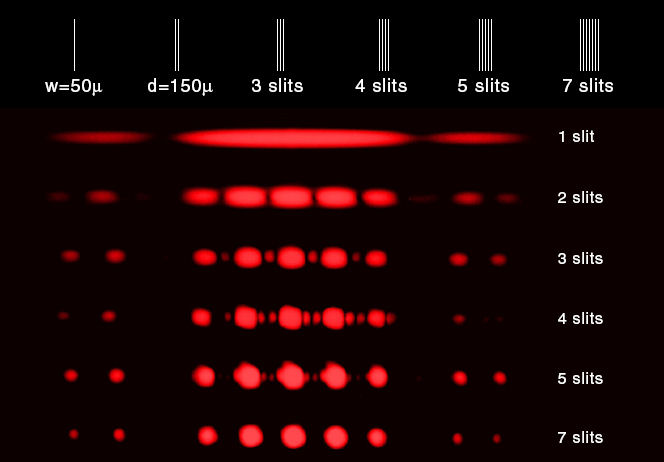
And here you can see how the pattern changes progressively as more slits are added to a barrier.
Diffraction Gratings 🔗
- Instead of having two slits, diffraction gratings often have tens, hundreds or thousands
- Their spacing is typically extremely small, this means the spacing between fringes is much larger than double-slits
- The slits are extremely thin, so the light is diffracted over almost 180 degrees
- There are a large number of slits, so interference is predominantly destructive, with small areas of constructive interference.
- In the case of white light, within each fringe (n) the individual wavelengths are also split up
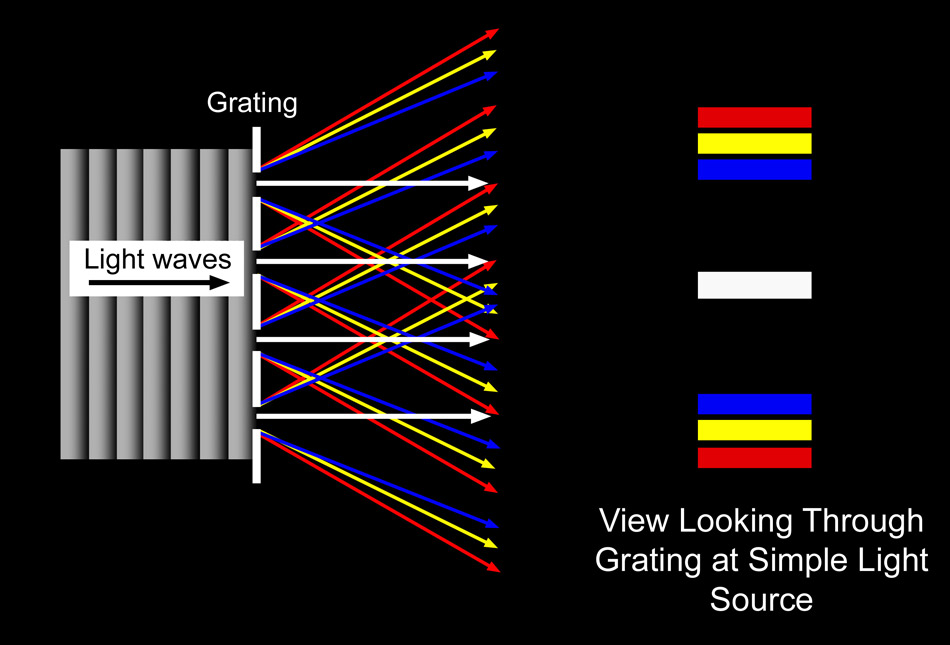
Colours 🔗
- We should notice, as mentioned before, red light diffracts the most and blue/purple the least. This means for each fringe red is on the outside and blue/violet on the inside.
- For the central white fringe, each different wavelength has arrived in-phase ($pd=n\lambda$), therefore their antinodes recombine into white light.

Task 🔗
Diffraction gratings cloze. Collect one, glue it in and fill in the blanks.
Doing Calculations 🔗
- We can still use our equations from before $pd = dsin(\theta)$
- However, diffraction gratings are typically described like this: “2000 lines per cm”. We need to calculate $d$, slit separation, from this number.
Pātai 🔗
Calculate the slit separation for a grating with 2000 lines per cm.
Whakatika 🔗
Because there are 2000 lines (gaps) in $1cm$, we can simply divide them to find the distance between each gap.
$$ \begin{aligned} d &= \frac{1cm}{2000 lines} \newline d &= 5\times10^{-4}cm \newline d &= 5\times10^{-6}m \end{aligned} $$
Pātai 🔗
Calculate the slit separation for a grating with 120,000 lines per $2.5cm$.
Whakatika 🔗
$$
\begin{aligned}
d &= \frac{2.5cm}{120000 lines} \newline
d &= 2.083\times10^{-5}cm
\end{aligned}
$$
Practice 🔗
- Textbook Activity 4C: Diffraction Gratings Q1,2 (and more)
- Homework Booklet Q16