Ngā Whāinga Ako ^🔗

• Be able to calculate the frequency of beats

Recall: Interference ^🔗

• When waves intersect each other, they interfere. This is where the amplitudes of the waves are combined (add positive and negative amplitudes).
• Constructive Interference: When two peaks meet and the resulting amplitude is greater
• Destructive Interference: When a peak and a trough meet and the resulting amplitude is less (or in some cases, zero)

Beats ^🔗

A periodic change in loudness of a sound.

• Produced when waves with similar frequencies interfere.
• Waves with different frequencies will slowly change their alignment (phase) over time, thus causing the interference to change.

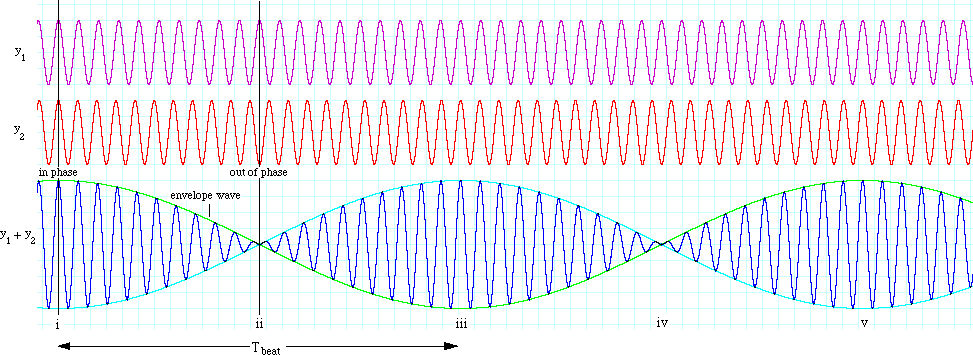
• Observation 1: The two waves (y1, y2) have a high frequency
• Observation 2: The beat they produce has a much lower frequency

This is due to y1 and y2 being very close in frequency.

Beat Frequency ^🔗

For beats to occur we need:

1. The amplitude to be the same
2. The difference in frequency to be small

$$ \begin{aligned} f_{b} &= |f_{2} - f_{1}| \end{aligned} $$

This equation is not given on your your formula sheet.

Pātai Tahi ^🔗

Zak is standing still and holding a device emitting a frequency of $100Hz$. Josh stands next to him holding a device emitting a frequency of $107Hz$.

Calculate the frequency of the beats observed by them both.

Whakatika Tahi ^🔗

This equation $f_{b} = |f_{2} - f_{1}|$ mainly tells us that the beat frequency is the absolute difference between the two frequencies.

$$ \begin{aligned} f_{b} &= f_{b} = |f_{2} - f_{1}| \newline f_{b} &= |100 - 107| = 7Hz \newline f_{b} &= |107 - 100| = 7Hz \end{aligned} $$

Pātai Rua: Piano Key ^🔗

Jules is tuning the middle C key on a piano. He is using a tuning fork which produces a frequency of $257Hz$ as a reference. The key is slightly out of tune and a beat frequency of $4Hz$ is heard.

Calculate the frequency of the out of tune key. Note any stumbling blocks you encounter!

Whakatika Rua ^🔗

$$ \begin{aligned} f_{b} &= |f_{2} - f_{1}| \newline 4 &= 257 - f_{k} = 253Hz \newline 4 &= f_{k} - 257 = 261Hz \end{aligned} $$

On paper we cannot tell which of the frequencies the key should have. In person, someone with a good musical ear could tell if the key is sharp (high) or flat (low).

Practice ^🔗

• P3.3 Worksheet #2 Q2b, c, d
• P3.3 Worksheet #2 Q5
• P3.3 Worksheet #2 Q4
• P3.3 Worksheet #2 Q3