Ohm’s Law and Power
12PHYS - Electricity
Finn Le Sueur
2024
Mahi Tuatahi / Do Now
Homework booklet Electric Fields Question Five
So far we have covered the concepts of:
- Charge carriers (electrons or otherwise),
- movement of charge carriers as current,
- charge carriers as the movers of energy,
- voltage as a difference in electric potential energy.
Pātai: What is the third variable that we are missing?
Resistance
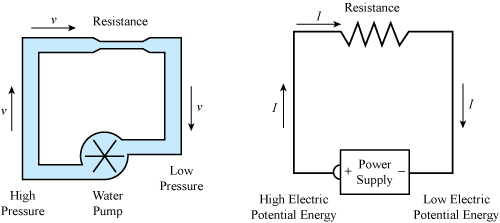
- Charge carries want to move around a circuit, and in a conductor they can do this easily due to the mobile electrons.
- In insulators they are not as able to move due to the less mobile electrons.
- Resistance is the idea of a friction that the current encounters that reduces the current able to flow, and causes energy to be lost/used as heat/light.
- In reality, everything is a little bit of a resistor.
Symbol & Units
- Resistance has symbol R in equations and has the unit Ohms (\(\Omega\), the Greek letter omega).
- Resistance changes when circuit components are added/removed or when a rheostat (variable resistor) is altered
- If supply voltage is constant, the current will increase/reduce as the resistance changes.
Resistance & Heat
When current moves through a material with resistance the electrons bump into other atoms. This causes energy to be transferred in the form of vibrations (heat)!
- The higher the resistance, the more heat produced!
- The higher the current, the more heat produced!
Ohm’s Law
\[ \begin{aligned} V &= IR \newline voltage &= current \times resistance \end{aligned} \]
- Voltage is measured in:
- Current is measured in:
- Resistance is measured in:
Pātai
- The resistance of a light bulb is \(1.5k\Omega\). Calculate the current through the bulb when it is connected across a \(12V\) power supply.
- When \(9V\) is applied to a resistor, \(0.03mA\) of current flows through it. Calculate the resistance of the resistor.
- How much voltage is required to produce \(180\mu A\) of current flowing through a \(0.6M\Omega\) resistor?
Whakatika Tahi
The resistance of a light bulb is \(1.5k\Omega\). Calculate the current through the bulb when it is connected across a \(12V\) power supply.
\[ \begin{aligned} & V = IR \newline & I = \frac{V}{R} \newline & I = \frac{12}{1500} \newline & I = 0.008A \end{aligned} \]
Whakatika Rua
When \(9V\) is applied to a resistor, \(0.03mA\) of current flows through it. Calculate the resistance of the resistor.
\[ \begin{aligned} & V = IR \newline & R = \frac{V}{I} \newline & R = \frac{9}{0.00003} \newline & R = 300000\Omega \end{aligned} \]
Whakatika Toru
How much voltage is required to produce \(180\mu A\) of current flowing through a \(0.6M\Omega\) resistor?
\[ \begin{aligned} & V = IR \newline & V = (180 \times 10^{-6}) \times (0.6 \times 10^{6}) \newline & V = 108V \end{aligned} \]
Power
Similar to Mechanics, power is defined as the amount of energy transferred (work done) per second, and is measured in \(Js^{-1}\) or \(W\).
\[ \begin{aligned} P &= IV \end{aligned} \]
The more power a component uses, the more energy is transformed (e.g. into light, heat, etc.)
Pātai
Revisit the three pātai you did just before and calculate the power dissapated (used) by the bulb and two resistors.
Confirming Ohm’s Law
- Collect a Confirming Ohm’s Law from the front.
- In small groups, set up a station with a hardmat to protect the bench.
- Vary the voltage across the resistor and record the current.
- Use the gathered data to complete Task 1-2.