Magnetic Fields and RH Slap Rule

Mahi Tuatahi

1. If an object has a charge of \(0.03C\), how many electrons has it lost?
2. There is \(80mA\) of current flowing through a \(2k\Omega\) resistor. How many electrons are going through the resistor in one second?
3. What is the power output of the resistor?

Whakatika Tahi

\[ \begin{aligned} & n = \frac{0.03}{1.6\times10^{-19}} \newline & n = 1.875\times10^{17} \end{aligned} \]

Whakatika Rua

\[ \begin{aligned} & I = \frac{q}{t} \newline & It = q \newline & q = 0.08 \times 1 = 0.08C \newline & n = \frac{0.08}{1.6\times^{-19}} = 5\times10^{17} \end{aligned} \]

Whakatika Toru

\[ \begin{aligned} & P = IV, V = IR\newline & P = I^{2}R \newline & P = 0.08^{2} \times 2000 = 12.8W (Js^{-1}) \end{aligned} \]

Pātai: What is an electric field?

Think, pair and share!

• A region in which a charged object experiences a force

What is a magnetic field?

• A region in which a moving charged object experiences a force

Magnetic Force: Particles

The force (\(F\)) that the charge experiences as it moves through the field depends on three things:

• Magnetic field strength (\(B\), measured in Tesla (\(T\)))
• Charge of the object (\(q\), measured in Coulombs (\(C\)))
• Velocity of the object (\(v\), measured in \(ms^{-1}\))

\[ \begin{aligned} F = Bqv \end{aligned} \]

Let’s summarise:

Electric Field: A region in which a charged object experiences a force \(F=Eq\)

Magnetic Field: A region in which a moving charged object experiences a force \(F=Bqv\)

Why Do Magnetic Fields Form?

• A model that will help us understand is as follows:
• The valence electrons of each atom have some small magnetic component to them
• When all of the atoms are aligned, their magnetic fields all add up to a much stronger/larger field

Ferromagnets and Paramagnets

• Ferromagnet: A material where the atoms are all aligned to create a permanent magnetic field
  • E.g. Iron, nickel, cobalt, and their alloys
• Paramagnets: A material with disorderly atoms, but that can become aligned when exposed to a strong external magnetic field.
  • E.g. Platinum, aluminium, oxygen, copper

Pātai

A narrow beam of protons (\(1.6\times10^{-19}C\)) moving at a speed of \(2.0\times10^{-6}ms^{-1}\), enters a uniform magnetic field of strength \(0.20T\).

Calculate the magnetic force applied on each proton.

Whakatika

\[ \begin{aligned} & F = Bqv \newline & F = 0.2 \times 1.6\times10^{-19} \times 2.0\times10^{-6} \newline & F = 6.4 \times 10^{-26}N \end{aligned} \]

Right-Hand Slap Rule (+ve Charges)

Thumb in the direction of positive charge velocity, finger-tips indicate the \(B\) field strength, and the palm shows the direction of force on the positive charge.

Back-Hand Slap Rule (-ve Charges)

Thumb in the direction of NEGATIVE charge velocity, finger-tips indicate the \(B\) field direction, and the back of the hand shows the direction of force on the NEGATIVE charge.

By default we use the +ve charge rule because we tend to think about conventional current (the flow of +ve charge).

Pātai

For each of these four situations, apply the RH rule and figure out what direction the current feels a force. Fingers go in direction of field and thumb in direction of current.

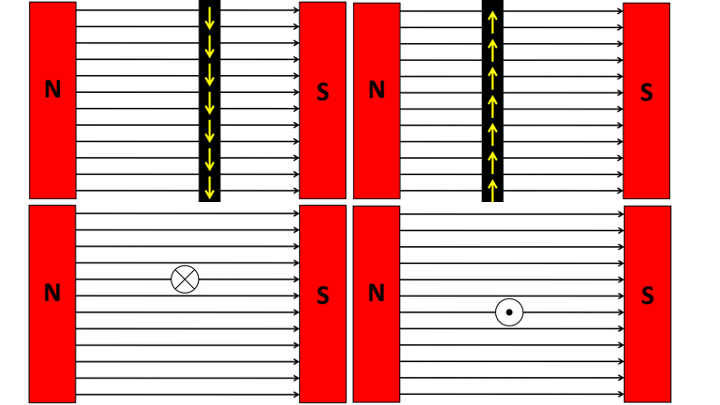
A cross means current going into the page down a wire; a dot means current coming out of the page.

Whakatika

1. Force out of the page
2. Force into the page
3. Force down
4. Force up

Pātai

A charged object (\(q=1.6\times10^{-19}C\)) moves to the left across a magnetic field (going bottom to top of the page) with a speed of \(4.0\times10^{3}ms^{-1}\). The magnetic field strength is \(12T\).

1. Draw a diagram and illustrate the magnetic field lines
2. Calculate the force applied to the charged object
3. Describe/draw the direction of the force applied

Cathode Ray Tube & Magnets

• Collect a Cathode Ray Tube and Magnets sheet
• Come up the front where you can observe the CRT monitor.
• Use our discussion and information at the top to answer Task 1-2.

Whakawai

Textbook page 235 Q1-2