Induced Voltage and Current

Pātai/Question

• Recall \(F=Bqv\)
• What happens if we take a wire and we move it through a magnetic field?

Whakatika

1. The charged particles (electrons) are now moving through an electric field, and therefore feel a force!
2. The force exerted on the moving electrons by the magnetic field will cause them to accelerate and therefore to move
3. If the circuit is complete:
   1. Moving electrons is known as a induced current!
   2. Moving electrons will cause an unequal distribution (difference in potential), known as induced voltage.

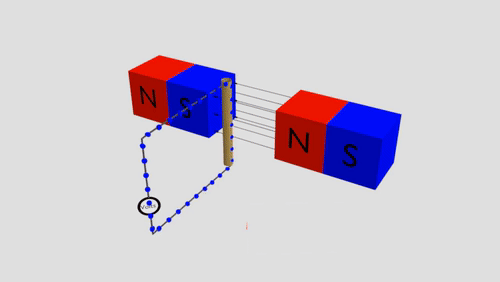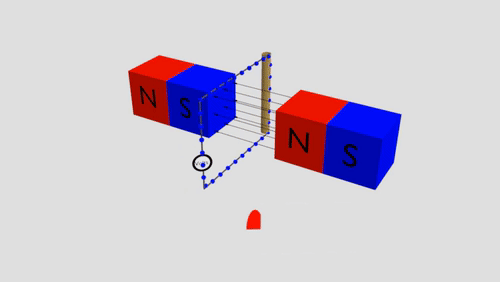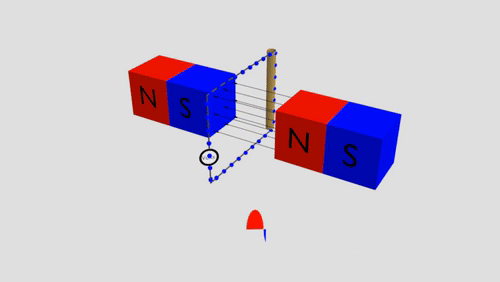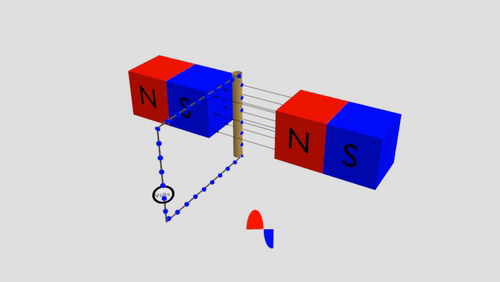
Inductors Summary

Moving charges through a magnetic field will cause them to feel a force (due to the magnetic field). Thus creating an induced voltage.

In a complete circuit, this is seen as a induced current.

Induced Voltage

Exists in a conductor moving through a magnetic field in a perpendicular direction.

\[ \begin{aligned} & V=BvL \end{aligned} \]

• \(V\) is the induced voltage (V, Volts)
• \(B\) is the magnetic field strength (T, Tesla)
• \(v\) is the velocity of the condutor (\(ms^{-1}\))
• \(L\) is the length of the condutor in the field (\(m\))

Pātai

A metal rod is moved in a magnetic field. The rod is \(24cm\) long and moves at \(8ms^{-1}\) through a magnetic field with strength \(0.7T\).

1. Calculate the induced voltage
2. Calculate the induced current and indicate direction

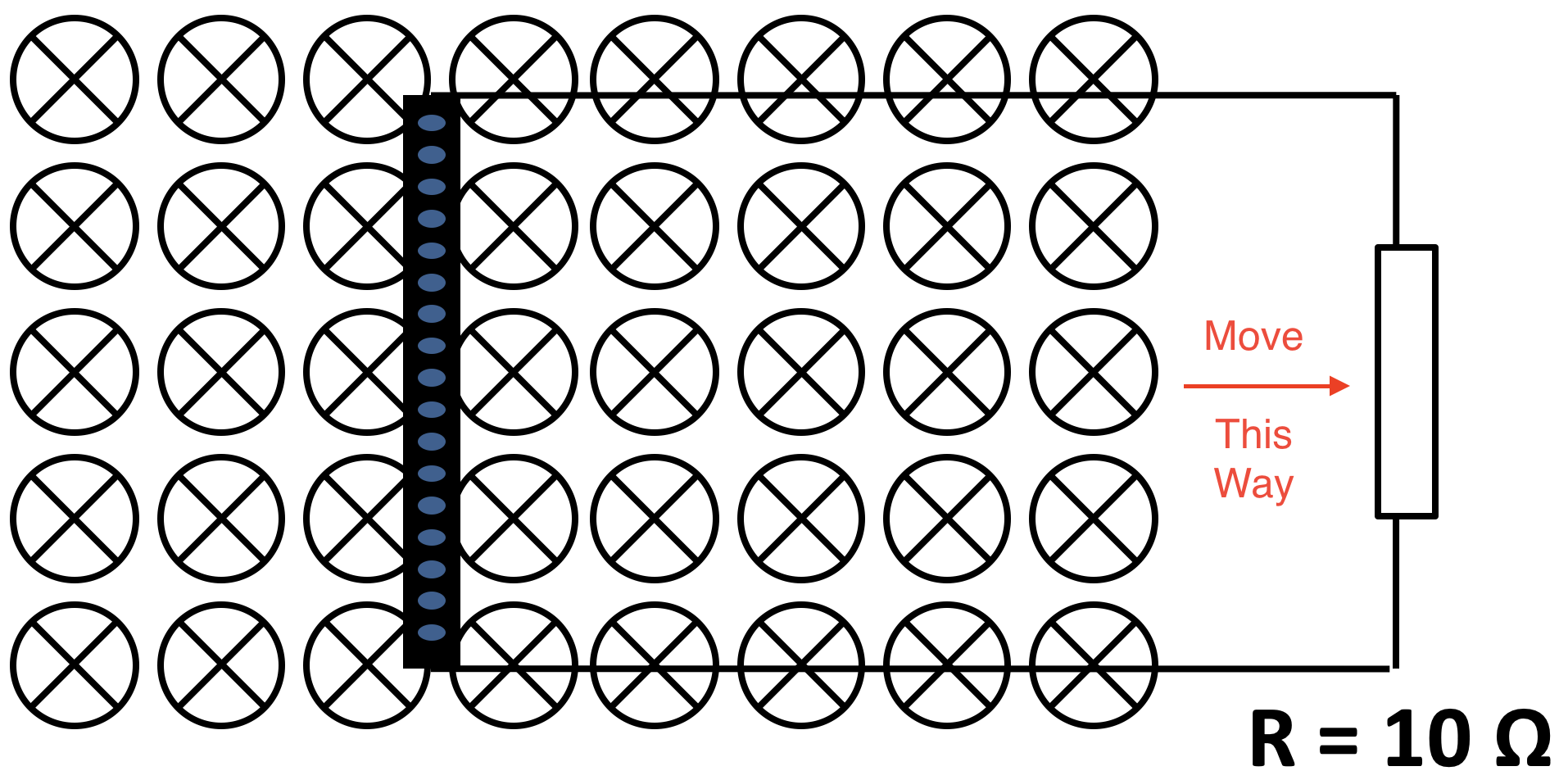
Whakatika

\[ \begin{aligned} & V = BvL \newline & V = 0.7 \times 8 \times 0.24 \newline & V = 1.344V \end{aligned} \]

\[ \begin{aligned} & V = IR \newline & I = \frac{V}{R} \newline & I = \frac{1.344}{10} = 0.1344A \end{aligned} \]