Mahi Tuatahi / Do Now ^🔗

Homework booklet Electric Fields Question Five

So far we have covered the concepts of:

• Charge carriers (electrons or otherwise),
• movement of charge carriers as current,
• charge carriers as the movers of energy,
• voltage as a difference in electric potential energy.

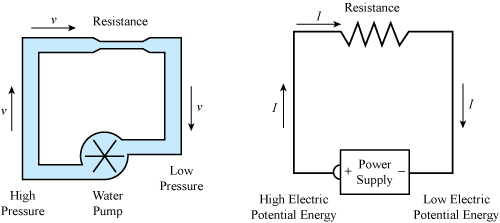
Pātai: What is the third variable that we are missing?

Resistance ^🔗

• Charge carries want to move around a circuit, and in a conductor they can do this easily due to the mobile electrons.
• In insulators they are not as able to move due to the less mobile electrons.
• Resistance is the idea of a friction that the current encounters that reduces the current able to flow, and causes energy to be lost/used as heat/light.
• In reality, everything is a little bit of a resistor.

Symbol & Units ^🔗

• Resistance has symbol R in equations and has the unit Ohms ($\Omega$, the Greek letter omega).
• Resistance changes when circuit components are added/removed or when a rheostat (variable resistor) is altered
• If supply voltage is constant, the current will increase/reduce as the resistance changes.

Resistance & Heat ^🔗

When current moves through a material with resistance the electrons bump into other atoms. This causes energy to be transferred in the form of vibrations (heat)!

• The higher the resistance, the more heat produced!
• The higher the current, the more heat produced!

Ohm’s Law ^🔗

$$ \begin{aligned} V &= IR \newline voltage &= current \times resistance \end{aligned} $$

• Voltage is measured in:
• Current is measured in:
• Resistance is measured in:

Pātai ^🔗

1. The resistance of a light bulb is $1.5k\Omega$. Calculate the current through the bulb when it is connected across a $12V$ power supply.
2. When $9V$ is applied to a resistor, $0.03mA$ of current flows through it. Calculate the resistance of the resistor.
3. How much voltage is required to produce $180\mu A$ of current flowing through a $0.6M\Omega$ resistor?

Whakatika Tahi ^🔗

The resistance of a light bulb is $1.5k\Omega$. Calculate the current through the bulb when it is connected across a $12V$ power supply.

$$ \begin{aligned} & V = IR \newline & I = \frac{V}{R} \newline & I = \frac{12}{1500} \newline & I = 0.008A \end{aligned} $$

Whakatika Rua ^🔗

When $9V$ is applied to a resistor, $0.03mA$ of current flows through it. Calculate the resistance of the resistor.

$$ \begin{aligned} & V = IR \newline & R = \frac{V}{I} \newline & R = \frac{9}{0.00003} \newline & R = 300000\Omega \end{aligned} $$

Whakatika Toru ^🔗

How much voltage is required to produce $180\mu A$ of current flowing through a $0.6M\Omega$ resistor?

$$ \begin{aligned} & V = IR \newline & V = (180 \times 10^{-6}) \times (0.6 \times 10^{6}) \newline & V = 108V \end{aligned} $$

Power ^🔗

Similar to Mechanics, power is defined as the amount of energy transferred (work done) per second, and is measured in $Js^{-1}$ or $W$.

$$ \begin{aligned} P &= IV \end{aligned} $$

The more power a component uses, the more energy is transformed (e.g. into light, heat, etc.)

Pātai ^🔗

Revisit the three pātai you did just before and calculate the power dissapated (used) by the bulb and two resistors.

Confirming Ohm’s Law ^🔗

• Collect a Confirming Ohm’s Law from the front.
• In small groups, set up a station with a hardmat to protect the bench.
• Vary the voltage across the resistor and record the current.
• Use the gathered data to complete Task 1-2.