Nuclear Fission and Fusion

Akoranga 9 Ngā Whāinga Ako

• Understand the difference between nuclear fission and fusion
• Use \(E=mc^{2}\)
• Use \(P=\frac{E}{t}\)

Recall

There are three types of nuclear reactions

1. Radioactive decay (\(\alpha\), \(\beta\), \(\gamma\))
2. Nuclear fission
3. Nuclear fusion

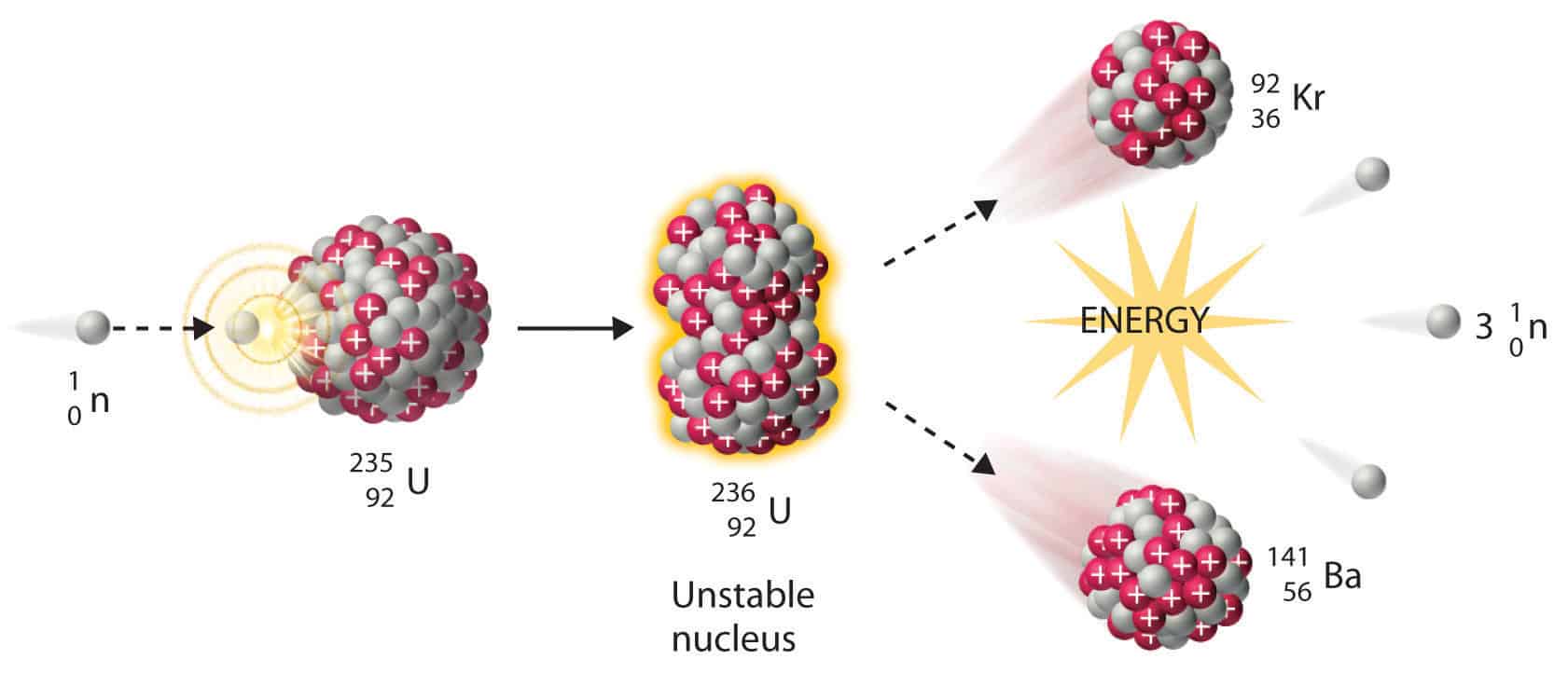
Fission

Question

If the protons are positively charged, why don’t they repel each other and the nucleus break apart?

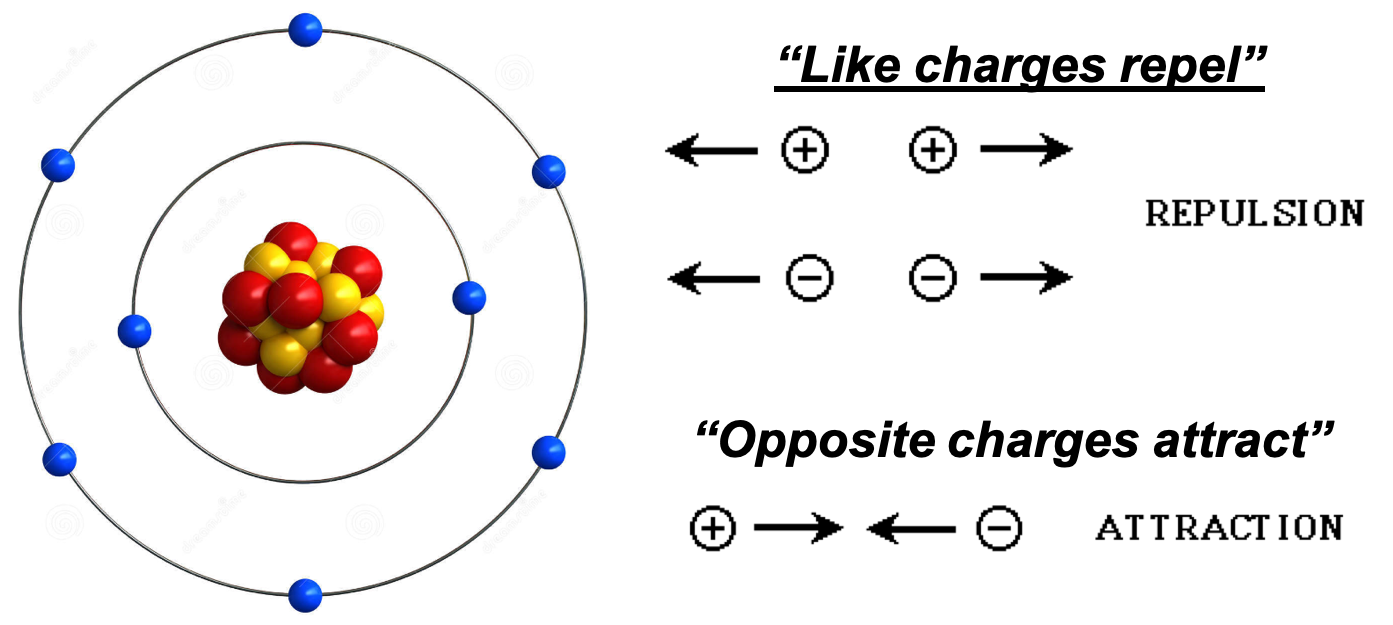
Electrostatic Force vs. Nuclear Force

• When nucleons are extremely close together, a very strong force called the Nuclear Force comes into effect.
• It is the nuclear force that holds the nucleons together and is stronger than the electrostatic force/repulsion between the protons.

Radioactive Isotopes

• Some isotopes, such as polonium-211, have unnaturally large numbers of nucleons in their nuclei.
• In these isotopes, the nuclear force holding the nucleons together is not enough to overcome the electrostatic repulsion between them (because there are too many) – making them unstable or radioactive

Absorption of a Nucleon

• If a fast moving nucleon can get extremely close to a nucleus of an atom, then the nuclear force will come into effect and it will be incorporated into the nucleus.
• This is easier to do with a neutron because neutrons have no charge so they do not experience any electrostatic repulsion (i.e. will not be repelled by protons).

Pātai: Write 2x nuclear equations to express this reaction

Whakatika

\[ \begin{aligned} & {}^{1}_{0}n + {}^{235}_{92}U \rightarrow {}^{236}_{92}U \newline & {}^{236}_{92}U \rightarrow {}^{92}_{36}Kr + {}^{141}_{56}Ba + 3{}^{1}_{0}n \end{aligned} \]

Extra pātai: What do you think the three neutrons produced do?

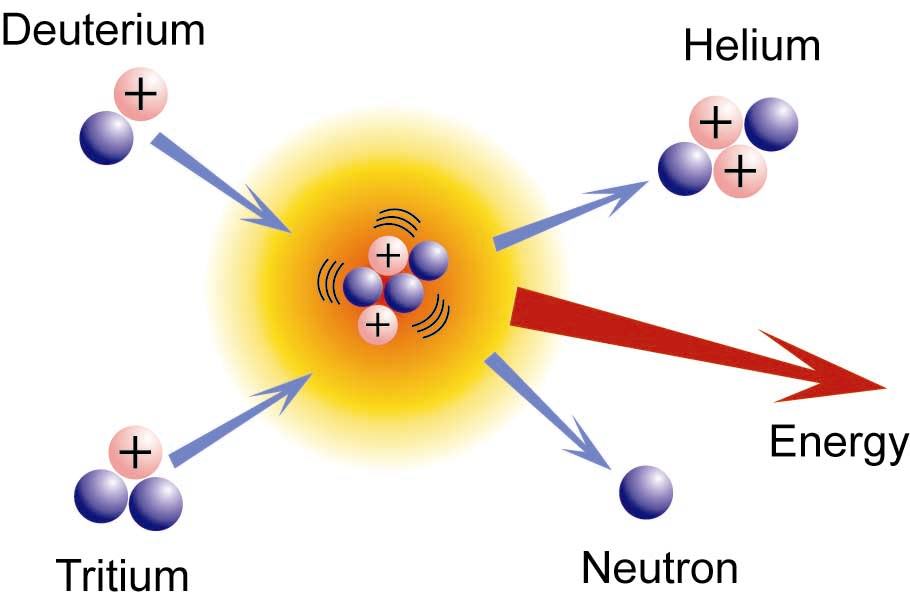
Whakatika

\[ \begin{aligned} & {}^{3}_{1}H + {}^{2}_{1}H \rightarrow {}^{4}_{2}He + {}^{1}_{0}n \end{aligned} \]

Producing Energy: Mass Balance

\[ \begin{aligned} & {}^{3}_{1}H + {}^{2}_{1}H \rightarrow {}^{4}_{2}He + {}^{1}_{0}n \end{aligned} \]

• Tritium (\({}^{3}_{1}H\)) \(= 5.00641 \times 10^{-27} kg\)
• Deuterium (\({}^{2}_{1}H\)) \(= 3.3436 \times 10^{-27} kg\)
• Helium (\({}^{4}_{2}He\)) \(= 6.64466 \times 10^{-27} kg\)
• Neutron (\({}^{1}_{0}n\)) \(= 1.67493 \times 10^{-27} kg\)

1. Calculate the total mass of the reactants.
2. Calculate the total mass of the products.

Theory of Relativity, \(E = mc^{2}\)

• Mass is a form of energy
• Mass can turn into energy and energy can turn into mass (in nuclear reactions).

During the fusion process, the total mass is not conserved because some of the mass of the fusing nuclei is converted to energy.

\[ \begin{aligned} & E = mc^{2} \end{aligned} \]

• \(E =\) energy
• \(m =\) mass
• \(c =\) speed of light (\(3\times10^{8}ms^{-1}\))

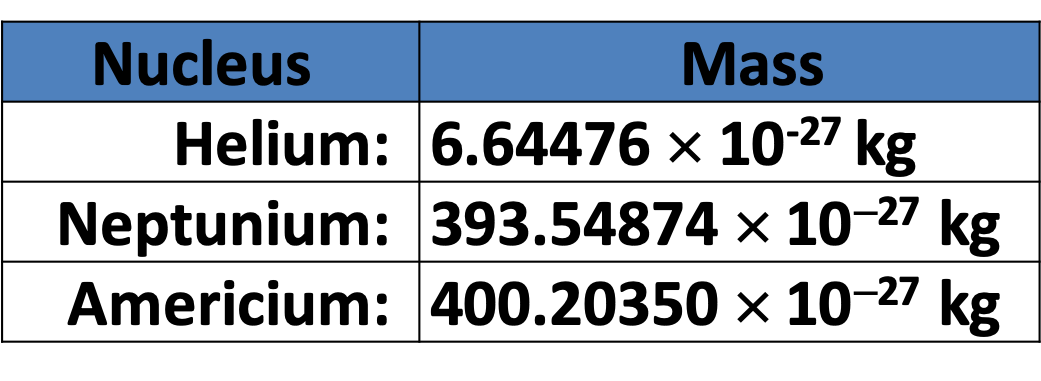
Pātai: Smoke Detector

• Americium-241 undergoes \(\alpha\) decay.
• 1. Write down the nuclear equation for the alpha decay of a nucleus of Americium-241.
• 2. Calculate the quantity of energy released when a nucleus of Americium-241 decays.

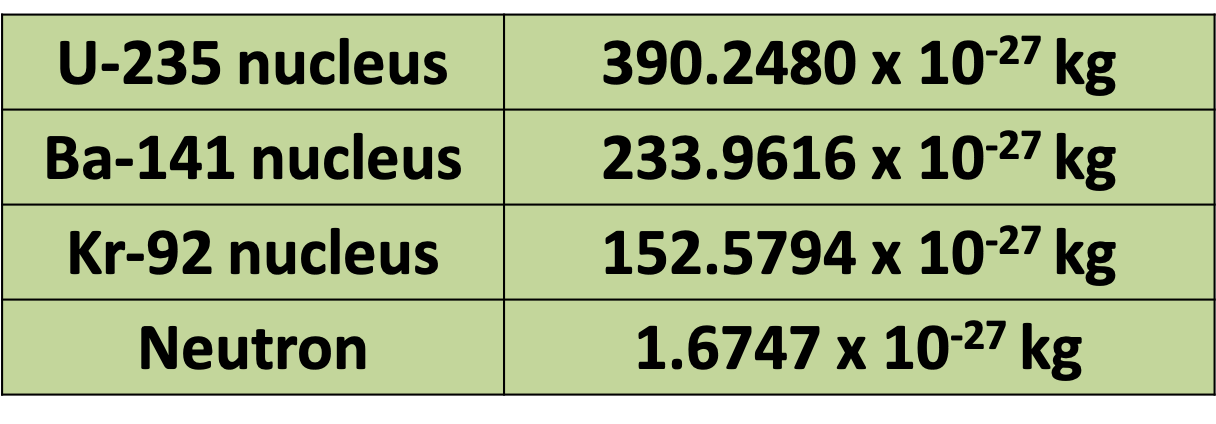
Pātai: Nuclear Fission

• In a fission reaction, an U-235 nucleus combines with a neutron, then splits into a Ba-141 nucleus, a Kr-92 nucleus and three neutrons. It also emits gamma radiation.
• Calculate the amount of energy released

Pātai: Nuclear Reactor

• A nuclear power plant in the US can produce one gigawatt of power using U-235.
• Calculate the mass of U-235 required each year to run the plant.

Tips for the Assessment

1. EXPLAIN your answers.
2. Watch out for the numbers NOT in standard forms (e.g. \(\times 10^{-27}\))
3. Half-life – Draw a graph!!!
   • Don’t forget about the shape of the exponential curve
4. Nuclear Equations – double check the atomic numbers and the mass numbers
5. \(E = mc^{2}\) – SHOW CLEAR WORKING