Akoranga 7 Mahi Tuatahi ^🔗

1. Date your book and collect a container of dice from the front
2. Count the total number of dice
3. Roll all the dice in one go. Set aside the dice with dots facing up, count the dice without dots and record that value.
4. Roll all the dice in one go that did did not land with dots facing up. Discard those with dots facing up, count, record and repeat until no dice remain.
5. Create a line graph showing the number of dice rolled (y-axis) vs the trial number (x-axis)

What you have graphed is an exponential decay curve! This is what nature does - we can observe it all over the place, even in electrical circuits.

It is not important to understand why at the moment, just to know that it does occur.

Mahi Tuatahi 2 ^🔗

1. A Carbon-14 nucleus emits a beta particle, then the daughter nucleus also emits a beta particle immediately after. Write two equations to show this.
2. An Uranium-241 nucleus emits an alpha particle AND a beta particle. Write down the equation.
3. An atom of Carbon-11 absorbs a neutron. Write down the nuclear equation.

$$ \begin{aligned} {}^{14}{6}C \rightarrow {}^{14}{7}N + {}^{0}{-1}\beta \newline {}^{14}{7}N \rightarrow {}^{14}{8}O + {}^{0}{-1}\beta \end{aligned} $$

$$ \begin{aligned} {}^{241}{92}U \rightarrow {}^{237}{87}Fr + {}^{4}{2}\alpha + {}^{0}{-1}\beta \end{aligned} $$

$$ \begin{aligned} {}^{11}{6}C + {}^{0}{1}n \rightarrow {}^{12}_{6}C \end{aligned} $$

Ngā Whāinga Ako ^🔗

• Be able to make half-life graphs
• Be able to interpret half-life graphs

Write ngā whāinga ako in your books

Half-Life ^🔗

The half-life is the time taken for half of the undecayed atoms in a sample to decay.

• Radioactive materials have unique half-lives.
• It is impossible to predict when an unstable/radioactive atom will disintegrate (decay), because the actual timing of the decay is random.

Tauira ^🔗

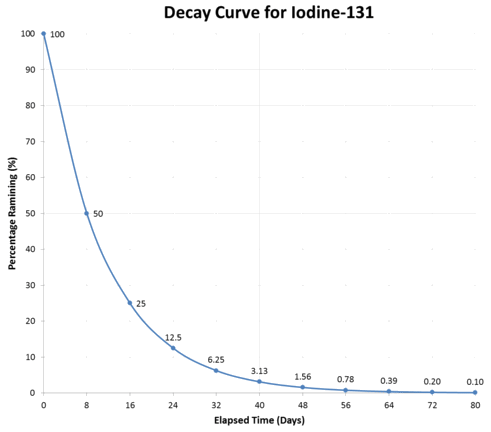
A small sample of a radioactive material iodine-131 has been observed for several days while it decayed into xenon-131. Read the below and determine its half-life.

• On the first day, the sample contained 40,000 iodine-131 nuclei.
• Eight days later, the sample only had 20,000 iodine-131 nuclei left.
• Another eight days later, the sample had 10,000 iodine-131 nuclei left.

Iodide-131 Half-Life Graph ^🔗

Pātai Tahi ^🔗

The half-life of Hydrogen-3 is approximately 12.25 years. If you found a small sample of Tritium containing 5,000,000 undecayed nuclei.

1. How many nuclei will be left after 12.25 years
2. How many nuclei will be left after 24.5 years
3. How many nuclei will be left after 49 years
4. How many nuclei will be left after 196 years
5. How long until there is less than 2500 undecayed nuclei left?

Whakatika Tahi ^🔗

1. 2,500,000
2. 1,250,000
3. 312,500
4. 76.29
5. Between 10-11 half-lives

Akoranga 8 Mahi Tuatahi ^🔗

You found a $50 g$ sample of Cobalt-60. The half-life of Cobalt-60 is 5 years. What would be the mass of the Cobalt-60 sample after 20 years?

1. Estimate how long it would take for the mass of the 50 g sample to fall just below $1.17 g$.
2. Sketch a mass vs. time graph of the Cobalt-60 sample over a 30-year period.
3. Use the graph to estimate the mass of the sample after 12.5 years.

Exponential Decay Curves ^🔗

• An exponential decay curve flattens out over time
• For any section, the graph is steeper on the left than the right
• This means, the mass/activity/number of atoms is changing more rapidly on left than the right

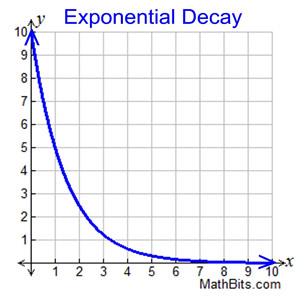
Predictions ^🔗

• If the dots were joined with straight lines, the mid-point should be half way
• But, because it is an exponential curve, the midpoint of nuclei remaining/mass/activity is actually slightly less than half way

Pātai: Predict time until 37.5% left ^🔗

Homework / Mahi Kāinga ^🔗

• Due Monday, marked and corrected
• Half-Life 2006 Q4, Atom Models Q4, Radioactivity Q8