Torque & Equilibrium
12PHY - Mechanics
Finn Le Sueur
2024
Mahi Tuatahi
\[ \begin{aligned} F=ma \end{aligned} \]
- State what each letter stands for
- Give the units for each letter
- Rearrange the equation for \(m\) and \(a\)
- Using the formula, what are the SI units for F (not Newtons)?
For a car of mass 1500kg which is accelerating at \(3.7ms^{-2}\):
- What net force is needed to maintain this acceleration?
\[ \begin{aligned} & && \text{Knowns} \cr & && \text{Unknowns} \cr & && \text{Formula} \cr & && \text{Sub and Solve} \end{aligned} \]
- If the engine is producing \(6000N\) of thrust, why is this different from your calculation?
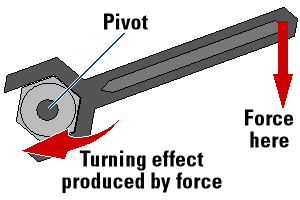
Torque (\(\tau\)) – Tōpana Whakahuri
Torque can be thought of as the turning effect around a pivot. Torque is sometimes known as moment or leverage.
\[ \begin{aligned} \tau &= Fd_{\bot} \cr torque &= Newtons \times metres \cr torque &= \text{Newton meters (Nm)} \end{aligned} \]
- \(F =\) force in Newtons
- \(d_{\bot} =\) perpendicular distance of force from pivot
Torque (\(\tau\)) – Tōpana Whakahuri
- A small force at a small distance produces a small torque,
- the same small force at a larger distance produces a larger torque.
- The force is in a straight line
- The torque is circular (CW or CCW)
Pātai: Individual Torques
- \(9N\) acting up at a distance of \(10cm\) is needed to lift the top off a bottle of soft drink. Calculate the torque applied.
- Calculate the torque applied if the lever is stretched to \(75cm\).
- Calculate the torque applied if the lever is compressed to \(1cm\).
\[ \begin{aligned} & && \text{Knowns} \cr & && \text{Unknowns} \cr & && \text{Formula} \cr & && \text{Sub and Solve} \end{aligned} \]
Pātai Whā: Does torque have a direction?
Yes, and you must always state which direction it is acting in.
Clockwise or Anticlockwise
Torque & Equilibrium

Equilibrium, Expanded
Newton’s First Law tells us equilibrium is when an object is at rest or moving uniformly (\(F_{net}=0\)).
For this to occur we need two things to be true. You must state these assumptions when doing any equilibrium question.
- Sum of all forces to be 0 (\(\sum F = 0N\))
- Sum of all torques to be 0 (\(\sum\tau = 0Nm\))
Pātai Tahi
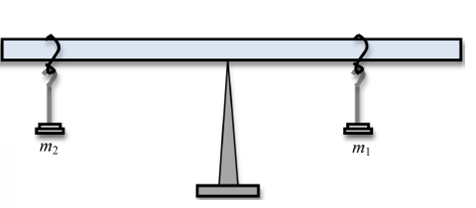
- \(m_{1}=2kg\), \(d_{1}=15cm\), \(m_{2}=1kg\), \(d_{2}=30cm\)
- Calculate the clockwise and anticlockwise torques
- Is the system in equilibrium?
Pātai Rua

- \(m_{1}=7kg\), \(d_{1}=36cm\), \(m_{2}=13kg\), \(d_{2}=65cm\)
- Calculate the clockwise and anticlockwise torques
- Is the system in equilibrium?
Mahi Tuatahi
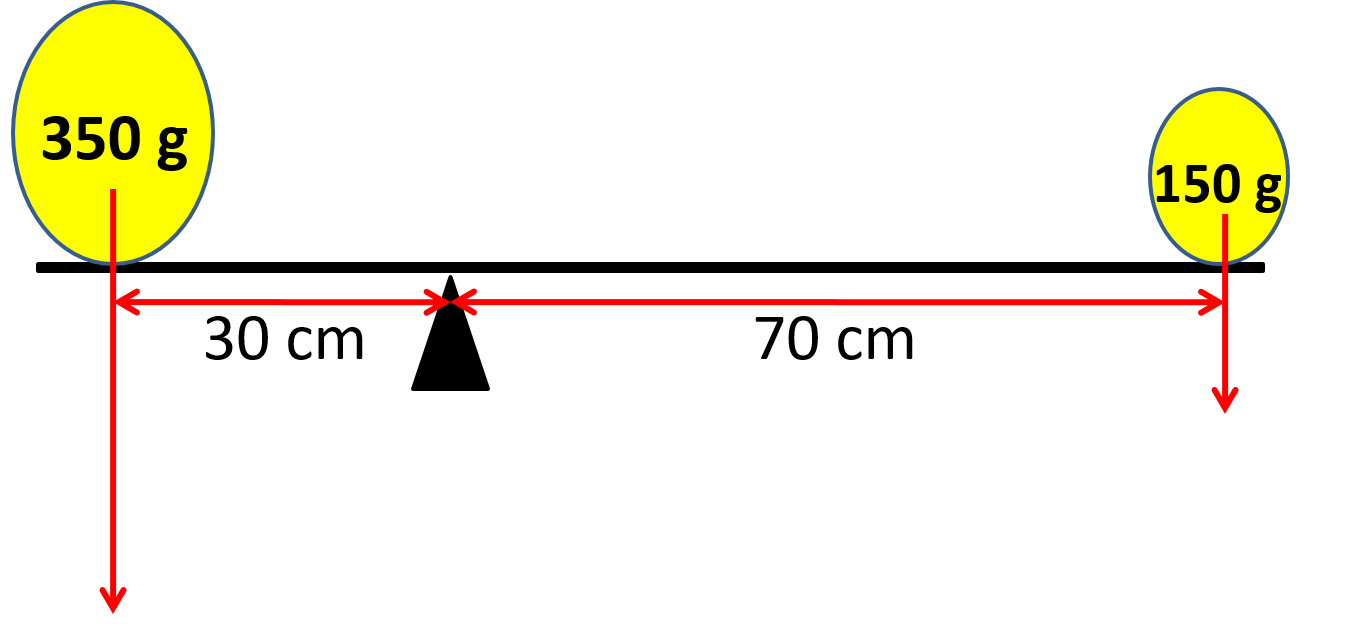
- Calculate the clockwise torque
- Calculate the anticlockwise torque
- Is it balanced?
Torque & Equilibrium
The plank may not be massless. You may need to take it into account.
- The mass of the plank acts through its centre of gravity
- Because the plank is uniform, this is the middle of the plank
How To Solve A Torque Problem
- Draw and label all forces on a diagram
- Draw and label the distances between all forces and the pivot
- Calculate all clockwise torque
- Calculate all anticlockwise torque
- Balance torques & forces
- Find the unknown value
Pātai: Balanced or Unbalanced?
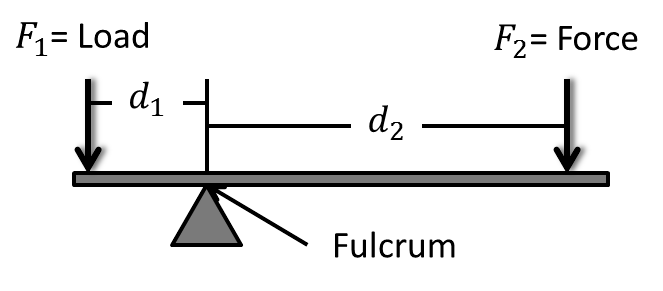
- \(d_{1}=30cm\), \(d_{2}=70cm\), \(m_{1}=900g\), \(m_{2}=300g\), see-saw mass = \(100g\).
- Is the system in equilibrium?
- Step 1: Calculate the total anticlockwise moment
- Step 2: Calculate the total clockwise moment
- Check if they are balanced.
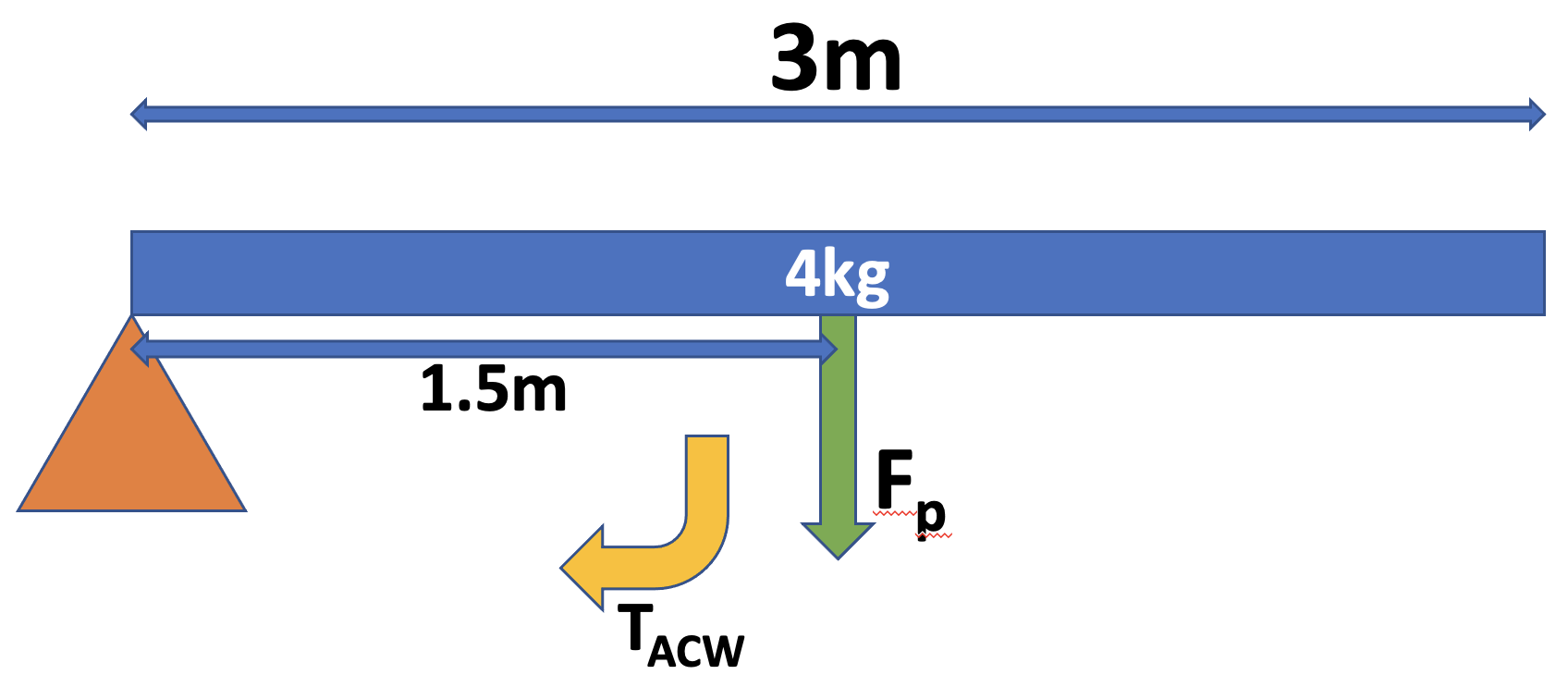
Pātai: Unknown Force

- Assume the system is in equilibrium (\(\tau_{clockwise} = \tau_{anticlockwise}\))
- \(d_{1}=0.5m\), \(d_{2}=1.5m\), \(F_{1}=2.5N\), see-saw mass = \(0.5kg\), \(F_{2}=?\).
- Draw the weight force of the see-saw on your diagram
- Find the unknown force, \(F_{2}\)
Whakatika
\[ \begin{aligned} \tau_{CW} &= \tau_{ACW} \cr \tau_{p} + \tau_{2} &= \tau_{1} \cr F_{p}d_{p} + F_{2}d_{2} &= F_{1}d_{1} \cr ((0.5 \times 9.8)\times 0.5) + F_{2}\times 1.5 &= 2.5 \times 0.5 \cr 2.45 + F_{2} \times 1.5 &= 1.25 \cr F_{2} &= \frac{1.25 - 2.45}{1.5} = -0.8N \end{aligned} \]
This is an interesting answer - it implies that \(F_{2}\) is actually acting up.
Pātai: Finding the Supports
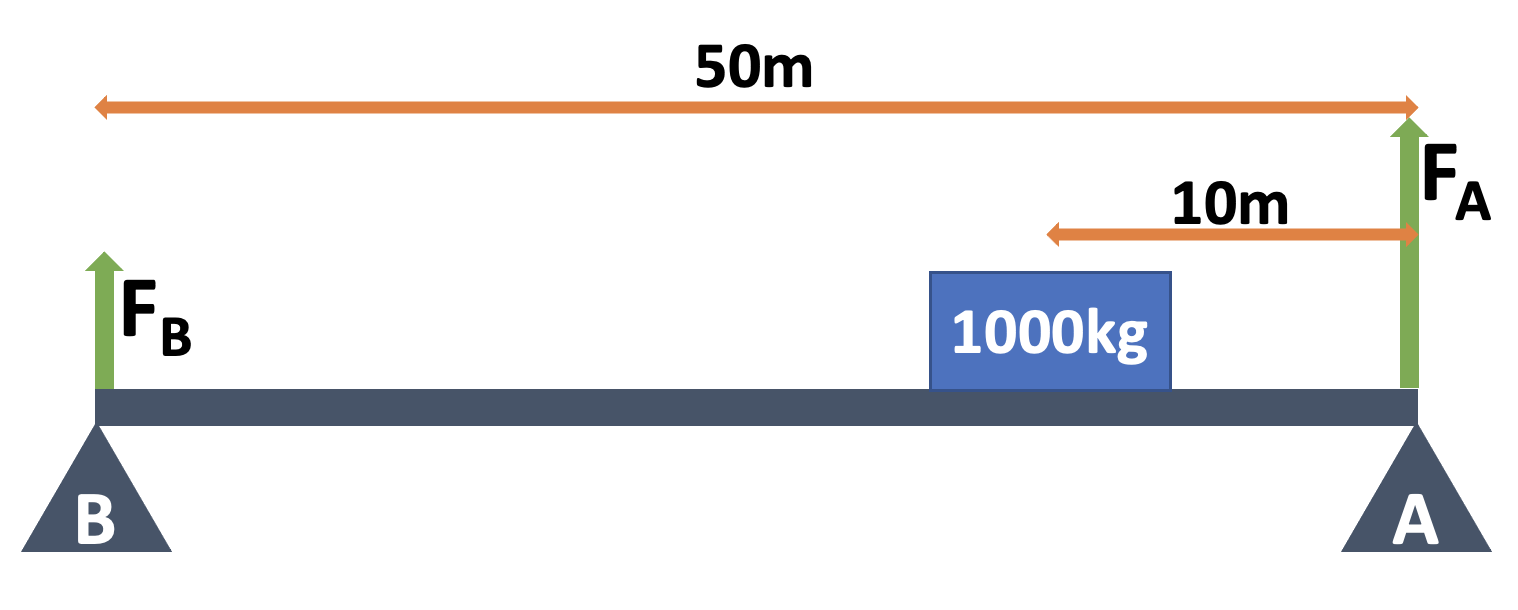
- Given that the bridge weighs \(10,000kg\), find the support force provided
by A and B.
- To find A, we make B the pivot. We also ignore \(F_{B}\) because it acting at the pivot and cannot provide any rotational forces.
- To find B, we make A the pivot. We also ignore \(F_{A}\) because it acting at the pivot and cannot provide any rotational forces.
- Solve for each support independently.
Whakatika: Support A
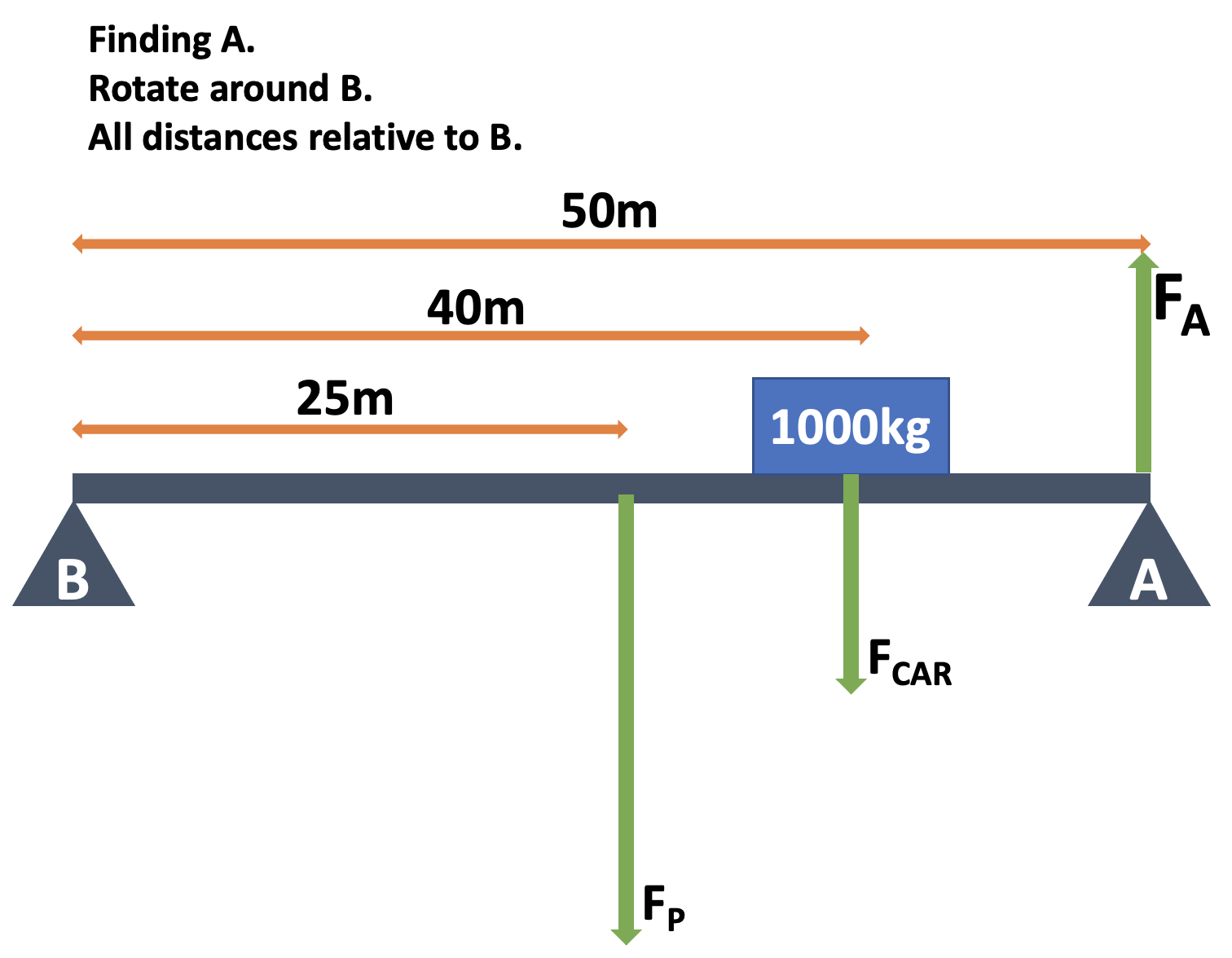
We are assuming the bridge is in equilibrium. This means that both net torque and net force are zero.
\[ \begin{aligned} \tau_{CW} &= \tau_{ACW} \cr \tau_{P} + \tau_{C} &= \tau_{A} \cr F_{P}d_{P} + F_{C}d_{C} &= F_{A}d_{A} \cr (m_{p}g)d_{p} + (m_{c}g)d_{C} &= F_{A}d_{A} \cr ((10,000 \times 9.8) \times 25) + ((1,000 \times 9.8) \times 40) &= F_{A} \times 50 \cr 2,450,000 + 392,000 &= F_{A} \times 50 \cr \frac{2,842,000}{50} &= F_{A} = 56,840N \end{aligned} \]
Whakatika: Support B
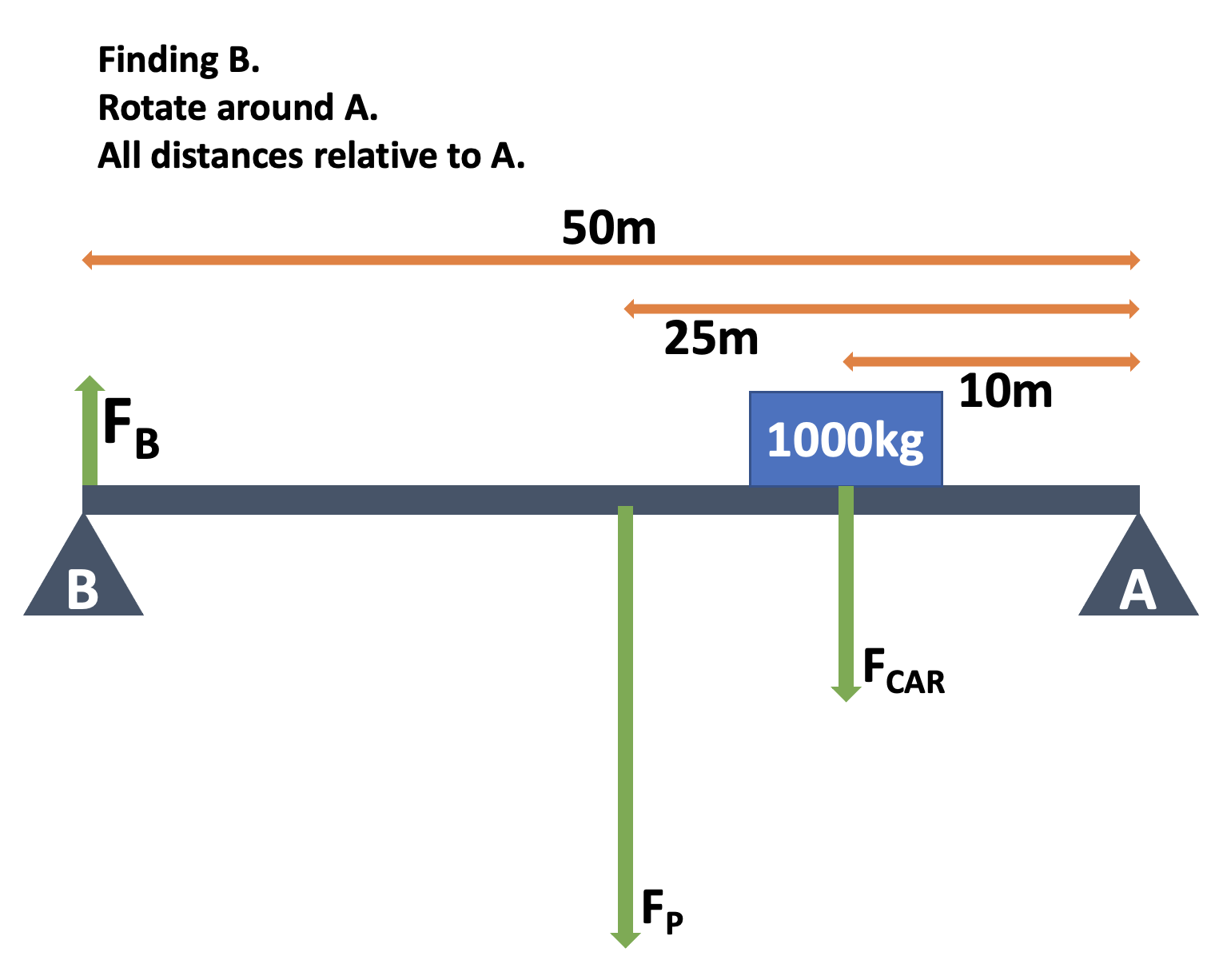
We are assuming the bridge is in equilibrium. This means that both net torque and net force are zero.
\[ \begin{aligned} \tau_{CW} &= \tau_{ACW} \cr \tau_{B} &= \tau_{P} + \tau_{C} \cr F_{B}d_{B} &= F_{P}d_{P} + F_{C}d_{C} \cr F_{B}d_{B} &= (m_{P}g)d_{P} + (m_{C}g)d_{C} \cr F_{B} \times 50 &= (10,000 \times 9.8 \times 25) + (1,000 \times 9.8 \times 10) \cr F_{B} \times 50 &= 2450000 + 98000 \cr F_{B} &= \frac{2,548,000}{50} = 50,960N \end{aligned} \]
Ngā Whakaaro / Thoughts
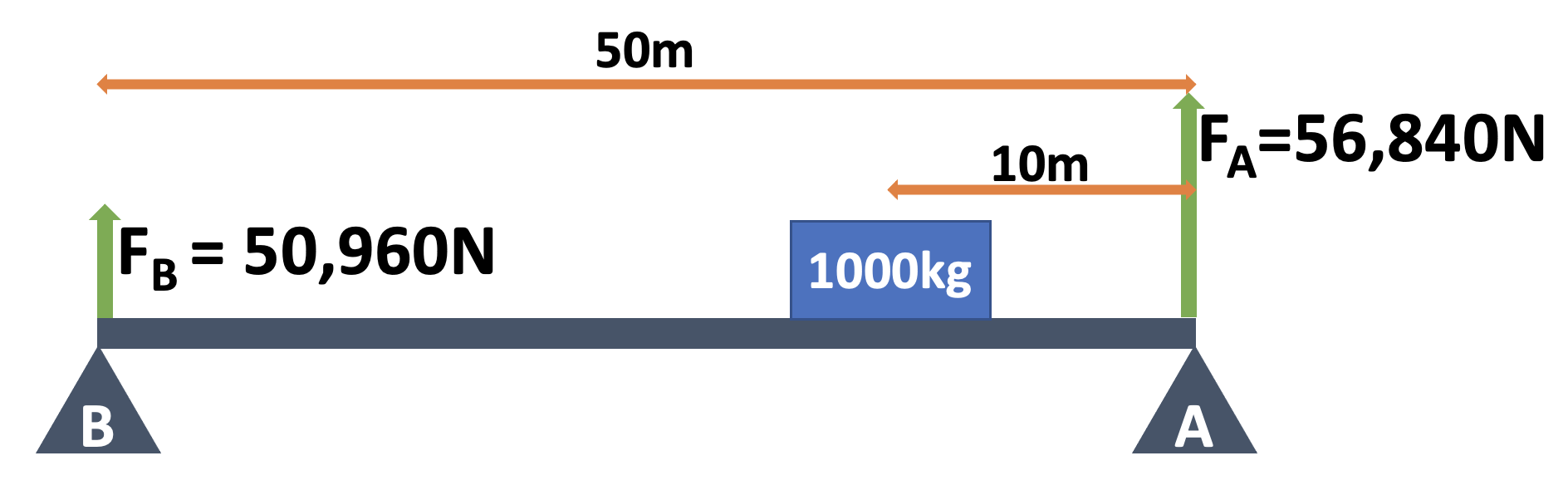
Because the car is closer to support B, it makes logical sense that support B should feel more of the weight force. Therefore, it needs to provide more support force in order to stay in equilibrium.
Whakawai / Practise
Textbook: Force, Equilibrium and Motion - Q7, 8, 10, 11, 12 Homework: Q41, Q43