Scalars vs Vectors
12PHYS - Mechanics
Finn Le Sueur
2024
Pātai: Scalars vs Vectors
In pairs, think about and discuss the similarities and differences between these two questions:
- Mr Chu puts 40 apples inside a box, except Miss Nam eats two of them. What is the total number of apples inside the box?
- Ms Carpenter lifts a plant off her desk with a force of \(15N\) in the upwards direction, while the plant has a weight force of \(5N\) acting down. What is the total force applied on the plant?
What is a Vector?
- Scalar = size only (e.g. mass)
- Vector = size and direction (e.g. velocity)
Discuss with your partner the difference between velocity and speed.
Example: Distance vs Displacement
- Distance is the amount an object
has moved
- It is a scalar
- E.g. 3km
- Displacement is the distance from
start to finish in a straight line
- It is a vector, because direction is also important
- E.g. 3km south west
Pātai
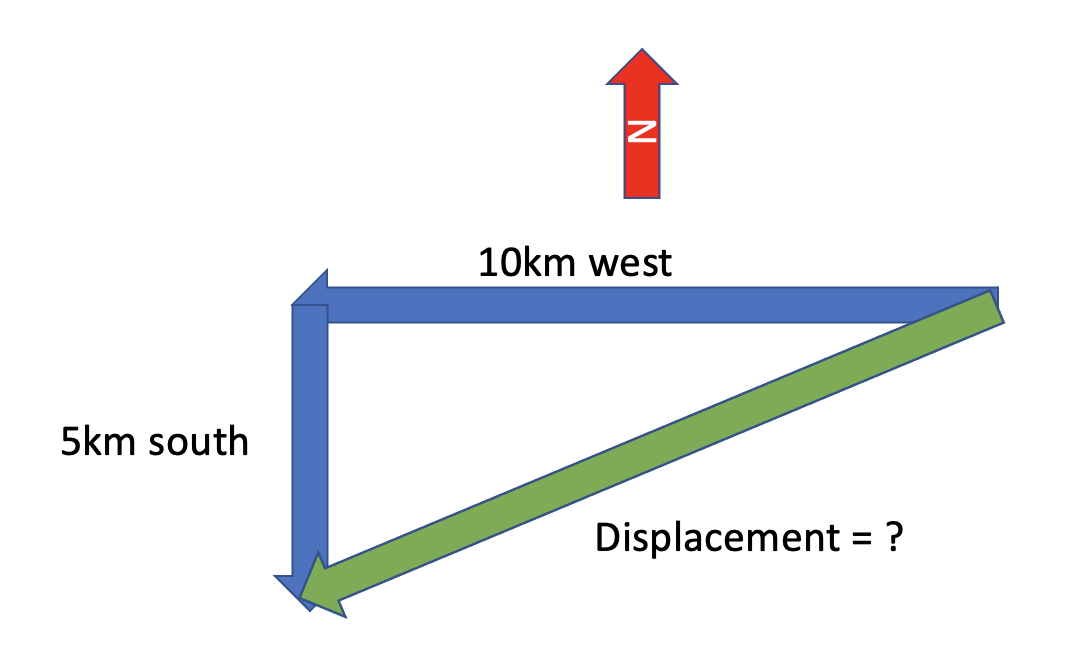
Ella drives to Sumner beach in the weekend because it is nice and hot outside. She drives \(5km\) south and \(10km\) west to get there.
- What is the total distance travelled by Ella?
- What is the total displacement of Ella?
Whakatika
- Distance: \(d = 5km + 10km = 15km\)
- Displacement: ?
Scalar or Vector?
- Distance
- Displacement
- Speed
- Velocity
- Acceleration
- Momentum
- Energy
- Force
- Temperature
- Mass
- Work
- Power
When dealing with problems which involve vector quantities (e.g. calculating velocity, force, etc.), you must consider the size and direction.
Which means: YOU MUST USE VECTOR DIAGRAMS (trigonometry) when working in two dimensions!
Vectors
- Have both direction and magnitude
- Drawn as an arrow
- Drawn with a ruler
- Drawn to scale (on a grid, typically)
- Drawn head-to-tail
- Can be added an subtracted
- Use Pythagoras and SOH CAH TOA to find values
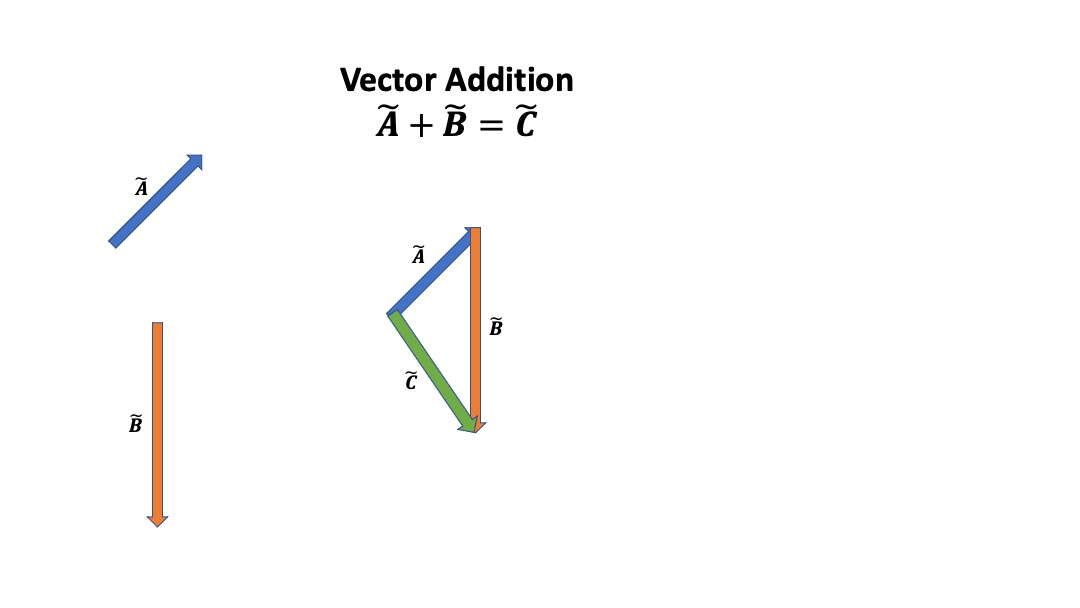
Vector Addition
- To add vectors, we simply draw a the next vector from the arrowhead of the previous one.
- Draw the resultant vector from start to finish in a separate colour.
- Important: The resultant vector should be pointing from start position to finish position
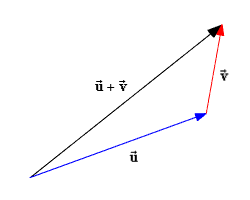
Why can’t we add vectors algebraically?
You help lift a box with a friend. You both apply 5N of force to lift
it. What is the resultant force? 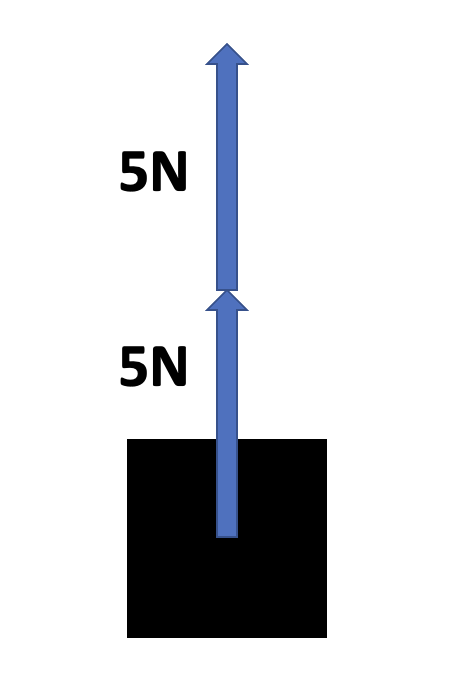
With a second box your friend pushes sideways with 5N of force while
you apply 5N up. What is the resultant force? Which direction is it
going? What is it’s size? 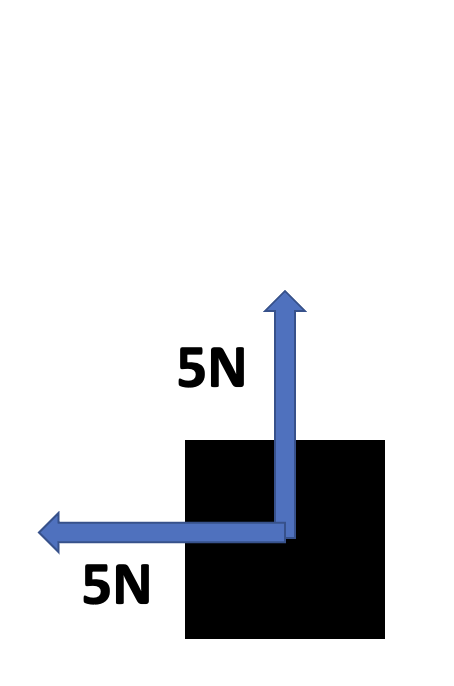
Vector Addition Example
A car is driven 3 km east for 200 seconds, then 4 km south for 250 seconds, then 3 km west for 150 seconds.
- What is the total distance the car has travelled?
- What is the total displacement of the car?
- What is the average speed of the car?
- What is the average velocity of the car?
\[ \begin{aligned} speed = \frac{distance}{time} \cr velocity = \frac{displacement}{time} \end{aligned} \]
Vectors Worksheet
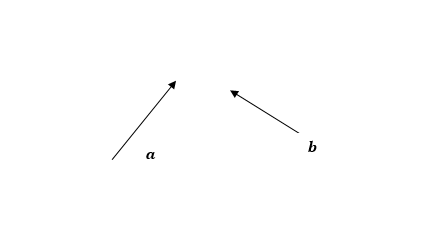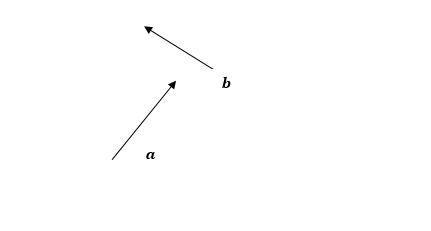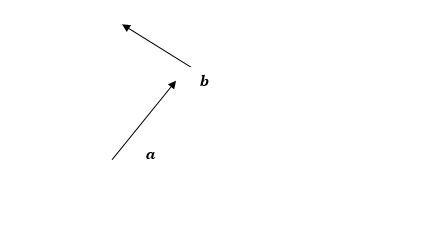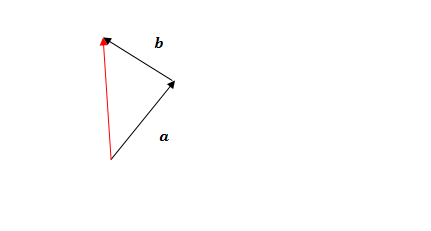
Mahi Tuatahi
Ngā Whāinga Ako
- Complete practical vector addition examples
- Introduce vector subtraction
- Calculate vector \(\Delta\)
Write the date and ngā whāinga ako in your book
Vector Subtraction
Consider acceleration:
- Positive acceleration will increase speed
- Negative acceleration will decrease speed
- Pātai: What is different?
- Whakatika: The direction of the acceleration!

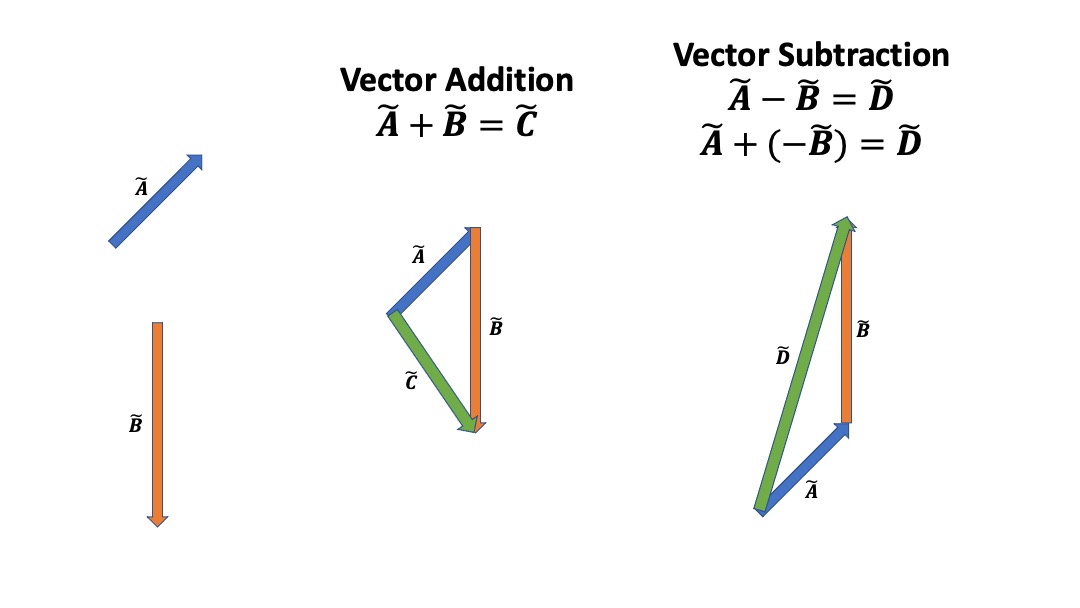
Summary: Vector subtraction is simply vector addition, where the subtracted vectors have their directions inverted.
Vectors with \(\Delta\)
Velocity is a vector and a change (\(\Delta\)) is calculated like this:
\[ \begin{aligned} \Delta v &= v_{f} - v_{i} \cr \end{aligned} \]
Pātai: Looks like vector subraction to me. Can we turn it into addition?
\[ \begin{aligned} & \Delta v = v_{f} - v_{i} \cr & \Delta v = v_{f} + (-v_{i}) \cr \end{aligned} \]
Example / Tauria
A soccer ball collides with the crossbar of a goalpost at \(5ms^{-1}\). It rebounds at \(4ms^{-1}\) in the opposite direction away from the crossbar.
- Draw a vector diagram illustrating this
- Determine the ball’s change in velocity using the
\(\Delta v\) equation
- Remember to use K,U,F,S,S
Practice / Whakawai
- ESA Activity 9A Q11-14
- Course Manual handout page 3-4
Mahi Tuatahi
- Mr Le Sueur walked his dog up Mt Barossa. He first walked 1.5km East in 30min and then 2.5km North in 1hr 15min. Draw a vector diagram of his displacement.
- Calculate his average speed
- Calculate his average velocity
- Give the direction of his displacement using an angle and a cardinal direction (e.g. 10 deg north of west).

Finding Directions
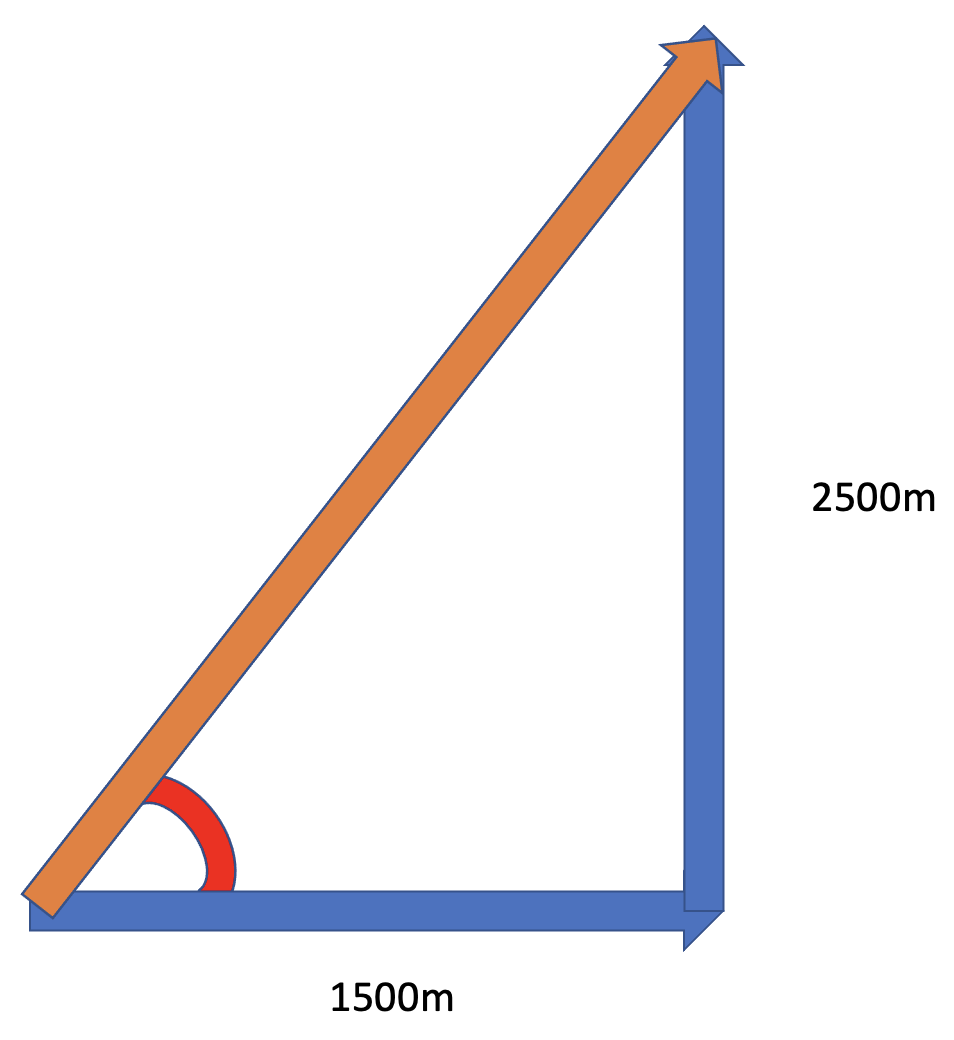
- SOH: \(sin(\theta) = \frac{opp}{hyp}\)
- CAH: \(cos(\theta) = \frac{adj}{hyp}\)
- TOA: \(tan(\theta) = \frac{opp}{adj}\)
Make sure your calculator is in degrees NOT radians!
Textbook Questions
- ESA Study Guide: Page 108-109, Q3, Q4, Q5, Q7, Q13.
- Extra: Homework booklet Q8
Mahi Tuatahi
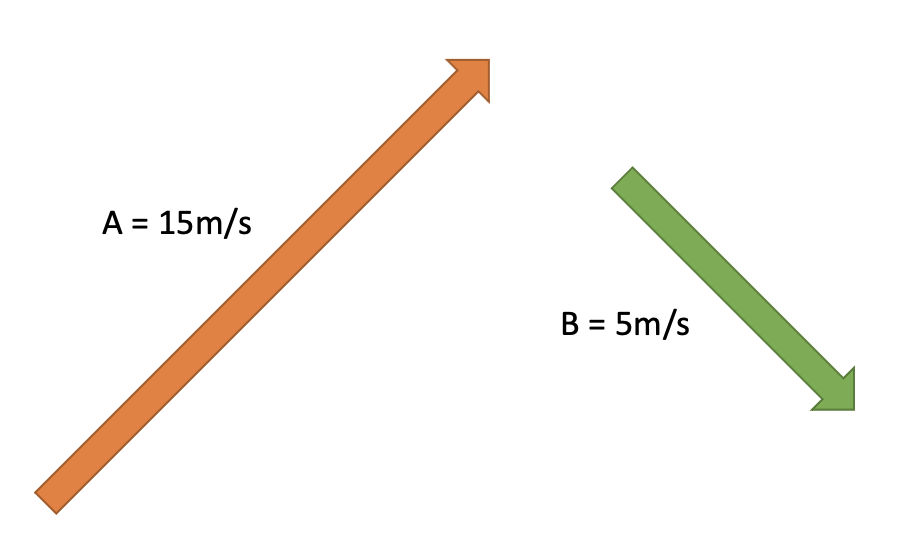
- Sarah passes the soccer ball to Kya at a speed of \(15ms^{-1}\). Kya then passes it off to Atua at a speed of \(5ms^{-1}\). Draw a vector diagram for this change in velocity.
- Calculate the change in velocity (remember Pythagoras)
- Calculate the angle of the change (remember SOH-CAH-TOA)
Answer / Whakatika
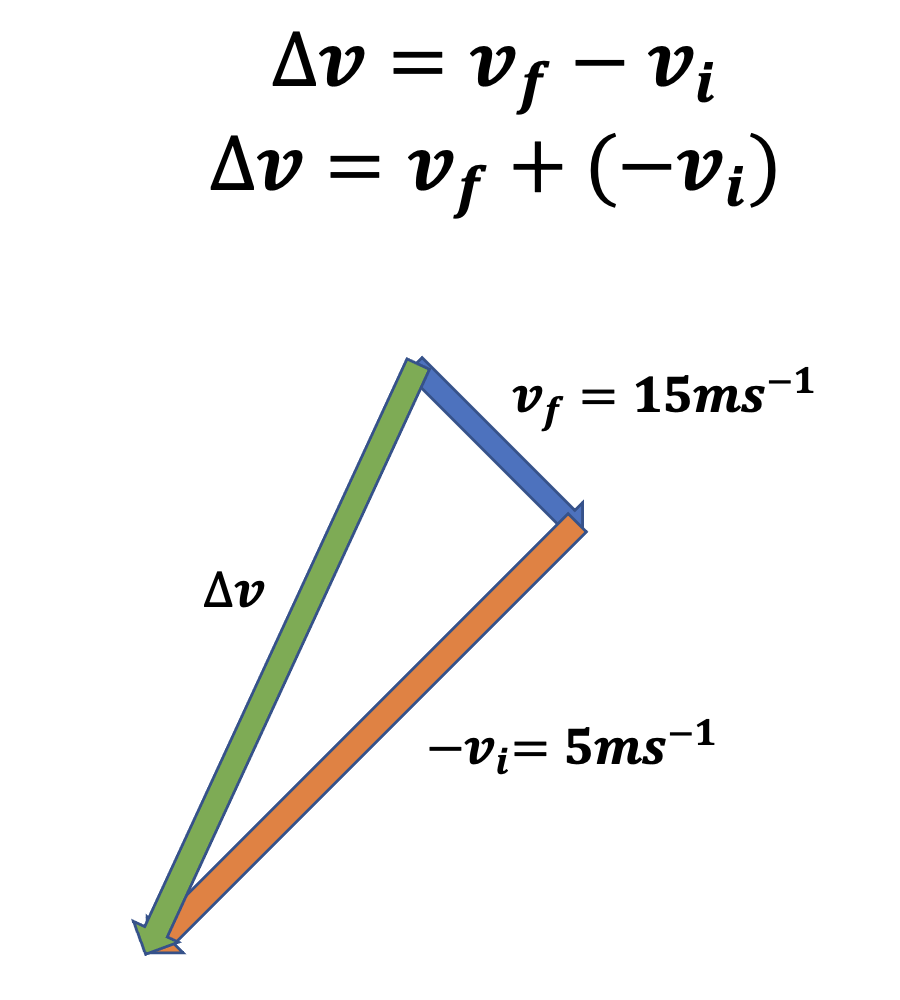
\[ \begin{aligned} \Delta v^{2} &= v_{f}^{2} + v_{i}^{2} \cr \Delta v &= \sqrt{v_{f}^{2} + v_{i}^{2}} \cr \Delta v &= \sqrt{15^{2} + 5^{2}} \cr \Delta v &= \sqrt{250} = 15.81ms^{-1} \cr\cr tan(\theta) &= \frac{opp}{adj} \cr \theta &= tan^{-1}(\frac{15}{5}) = 75.6\degree \end{aligned} \]
Te Whāinga Ako
- Decompose vectors into horizontal and vertical components
Write the date and te whāinga ako in your book
Vector Components
- Similarly to how we create a resultant vector by adding two vectors, we can decompose a vector on an angle into its horizontal and vertical components.
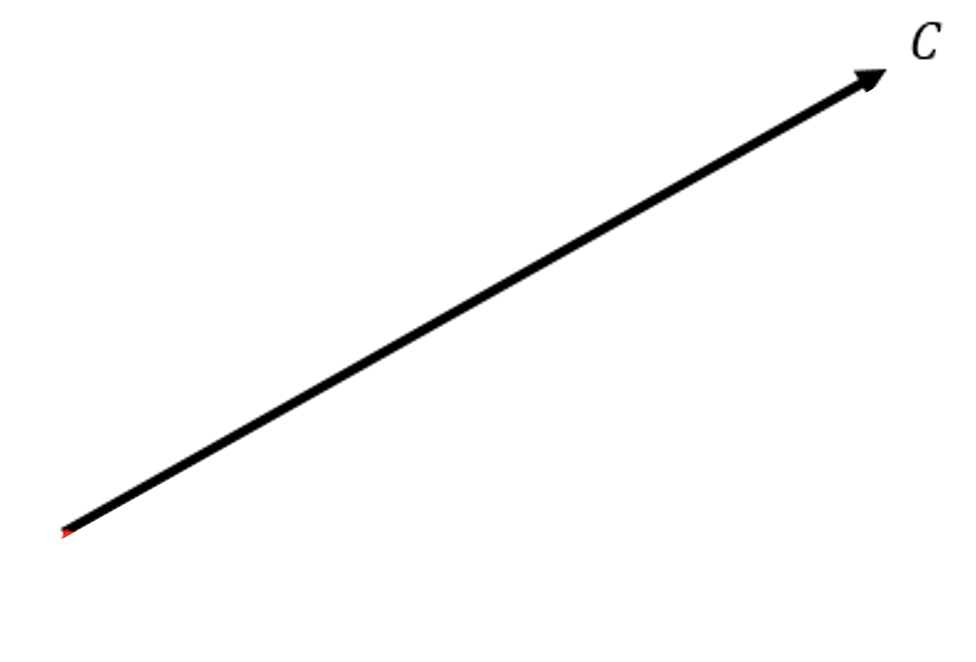
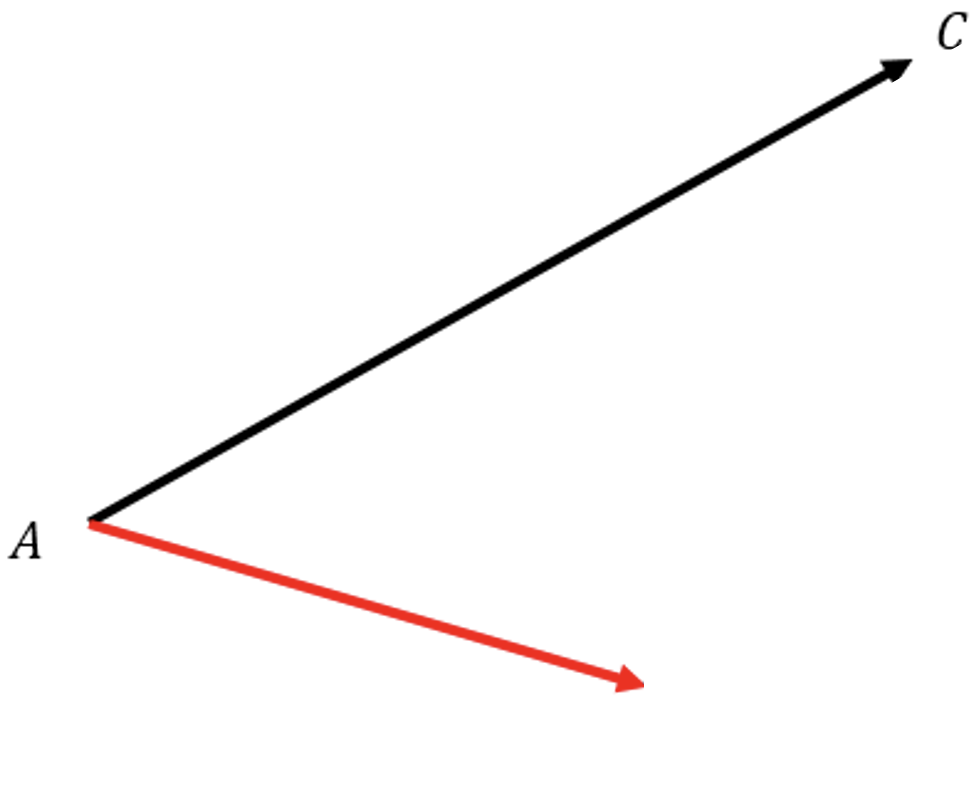
- Pātai: Draw two vectors which add together to result in \(\vec{C}\) (right-angled triangle).
Whakatika
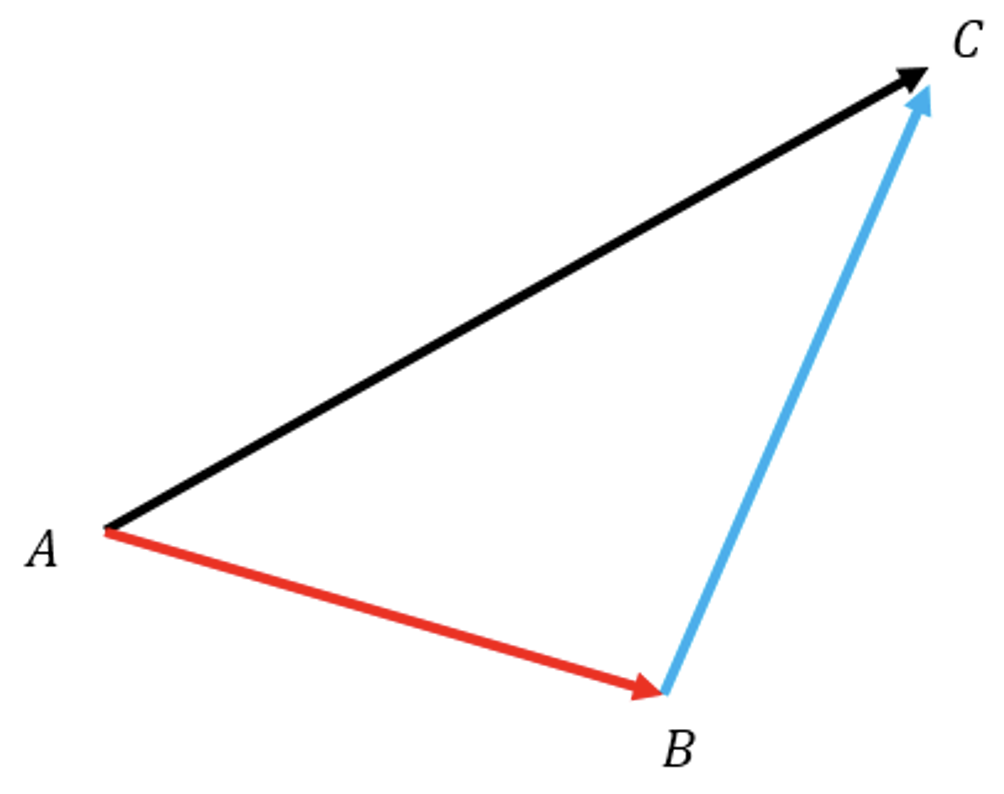
- This is an important skill because the x and y components of a vector are independent.
- This means they do not influence each other (e.g. in projectile motion)
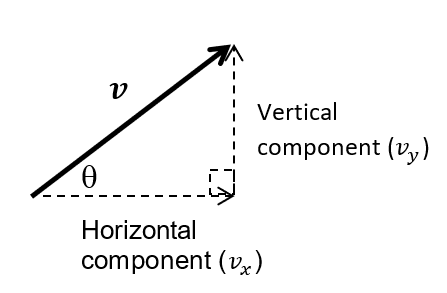
Pātai

- Mr Le Sueur tosses a ball across the classroom with an initial velocity of \(v=4ms^{-1}\) (hypotenuse), on an angle of \(40\degree\). Draw a labelled vector diagram
- Calculate the horizontal component of the velocity
- Calculate the vertical component of the velocity
Whakatika

\[ \begin{aligned} v_{x} &= v \times cos(\theta) && \text{Horizontal} \cr v_{y} &= v \times sin(\theta) && \text{Vertical} \end{aligned} \]
Textbook Pātai
- ESA Study Guide (2011): Page 108-109, Q1-14.
- ESA Study Guide (2008): Page 98-99, Q1-14.