Projectile Motion
12PHYS - Mechanics
Finn Le Sueur
2024
Mahi Tuatahi
- Yssy travels 30km south and then 20km west. Draw a vector diagram to show her total displacement (resultant).
- Max and Lena are pushing a box. Max is pushing it with force 500N to the right, and Lena is pushing it with force 400N up. Draw a vector diagram to show the net (resultant) force.
- Phoebe is flying at \(7ms^{-1}\) east. Phoebe changes direction so she flying at \(7ms^{-1}\) south. Draw a vector diagram and calclate her change in velocity.
Te Whāinga Ako
- Be able to describe the motion of an object undergoing projectile motion.
Write the date and te whāinga ako in your book
Whakamātau/Experiment
- How many seconds was the student in the air for?
- What is the acceleration due to gravity?
- What was their velocity at the top of their flight?
- How far up did Hancock throw them?
Projectile Motion
Parabolic motion due to gravity. Friction forces are ignored. Gravity is the only force acting. Motion up and motion down are symmetrical.

Describing Velocity
We need to be able to describe the velocity and acceleration of an object in projectile motion.
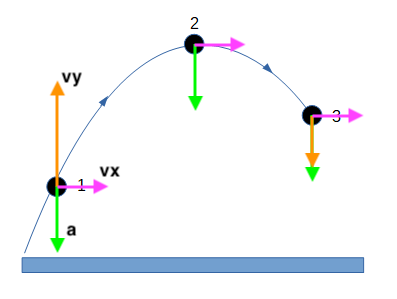
Forces on Projectiles
- We assume that friction force is negligible (we ignore it).
- Therefore, the only force acting upon the ball while in the air is the weight force.
- Weight force acts in the vertical direction only (\(a_{y} = g = 9.8ms^{-2}, v_{y} \ne const.\))
- No forces act in the horizontal (\(a_{x} = 0, v_{x}=const.\))

Acceleration Due to Gravity
\[ \begin{aligned} a = g = 9.8ms^{-2} \text{ (down)} \end{aligned} \]
Has the same magnitude at all points (\(9.8ms^{-2}\)) and always points downwards.

Projectile Motion: In Summary
- An object that moves through the air without its own power source;
- the only force acting upon it is the weight force;
- it is always experiencing downward acceleration of \(9.8ms^{-2}\);
- motion up/down is symmetrical.
- The path is follows is in the shape of a parabola.
Half-Projectile Motion: Pātai Tahi
A ball is thrown upwards with an initial speed of \(161.3kmh^{-1}\) (\(44.8ms^{-1}\)).
- How long does it take for the ball to reach its highest point?
- How high does the ball rise?
\[ \begin{aligned} & \textbf{1. Knowns} \cr & \textbf{2. Unknowns} \cr & \textbf{3. Formula} \cr & \textbf{4. Substitute} \cr & \textbf{5. Solve} \end{aligned} \]
Pātai Rua
Lachie kicks a rugby ball straight upwards. It is in the air for \(10.6s\) before it hits the ground.
- What is the initial velocity of the ball?
- If kicked towards some rugby posts, at its highest point, will it go over the crossbar (3m)?
\[ \begin{aligned} & \textbf{1. Knowns} \cr & \textbf{2. Unknowns} \cr & \textbf{3. Formula} \cr & \textbf{4. Substitute} \cr & \textbf{5. Solve} \cr \end{aligned} \]
Pātai Toru
Angus is going cliff diving. He jumps and falls for \(3.4s\) before hitting the water below.
- What is his initial velocity?
- What is his acceleration?
- What is his final velocity (as he hits the water)?
- How high is the cliff?
\[ \begin{aligned} & \textbf{1. Knowns} \cr & \textbf{2. Unknowns} \cr & \textbf{3. Formula} \cr & \textbf{4. Substitute} \cr & \textbf{5. Solve} \cr \end{aligned} \]
Whakawai/Practise
- Textbook Page 137: Activity 12A Q1, Q3
Full Projectile Motion
A cannon ball is fired horizontally from the top of a hill. The velocity of the cannon ball is split into \(x\) and \(y\) components, which are independent of each other.
- Weight force is the only force acting.
- The cannonball accelerates in the y direction (\(a_{y} = g = 9.8ms^{-2}\)).
- No forces are acting in the horizontal direction, so velocity is constant (\(a_{x} = 0\)).

Example / Tauria
A javelin is thrown at \(20ms^{-1}\) at an angle of \(30^{\circ}\) to the horizontal. What is it’s range?
- First, using trig, calculate the initial horizontal (\(v_{x}\)) and vertical (\(v_{y}\)) velocities
- Second, using vertical values, calculate the javelin’s time of flight
- Thirdly, using horizontal values, calculate the distance (range) of the javelin

Pātai: Hammer Throw
Hume throws a hammer as far as he can during the Highland Games. It has an initial velocity of \(12ms^{-1}\) on an angle of \(40^{\circ}\) to the ground. How far does it go?
- Separate the x and y values that you know.
- Calculate the x and y initial velocities (use a diagram).
- Calculate how long does it take for the projectile to reach the top of its path?
- What is the total time of flight?
- How far can it travel horizontally in that time?

Whakawai/Practise
- Worksheet #6 Projectiles
Three Types of Projectile Motion

You need to be able to solve all three types for the exam! We have covered Half and full parabolas so far, now we will do partial parabolas!.
Tauria / Example: Tossing a Ball
Ben kicks a ball to Elias who is standing \(12m\) away. Elias is \(180cm\) tall, and the ball has an initial velocity of \(7ms^{-1}\) at an angle of \(37^{\circ}\) to the horizontal. Does the ball travel over Elias’ head, hit them, or fall short?
- Calculate the x and y components of the initial velocity
- Think Horizontal: Calculate the time taking for the ball to reach Elias
- Think Vertical: What is the height (d) at time t (from above)?
- Turn your numerical answer into a sentence explaining what you found.
Whakatika
- Calculate the x and y components of the initial velocity
\[ \begin{aligned} v_{x} &= vcos(\theta) = 7cos(37) = 5.59ms^{-1} \cr v_{y} &= vsin(\theta) = 7sin(37) = 4.21ms^{-1} \end{aligned} \]
- Think Horizontal: Calculate the time taking for the ball to reach Elias
\[ \begin{aligned} &\text{K: } v_{xi} = 5.59ms^{-1}, a_{x} = 0ms^{-1}, d_{x} = 12m \cr &\text{U: } t = ? \cr &\text{F: } d = v_{i}t + \frac{1}{2}at^{2} \cr &\text{S: } 12 = 5.59 \times t + \frac{1}{1} \times 0 \times t^{2} \cr &\text{S: } \frac{12}{5.59} = t = 2.15s \end{aligned} \]
- Think Vertical: What is the height (d) at time t (from above)?
\[ \begin{aligned} &\text{K: } v_{yi} = 4.21ms^{-1}, a = 9.8ms^{-2}, t = 2.15s \cr &\text{U: } d = ? \cr &\text{F: } d = v_{i}t + \frac{1}{2}at^{2} \cr &\text{S: } d = (4.21 \times 2.15) + (0.5 \times -9.8 \times 2.15^{2}) \cr &\text{S: } d = -13.60m \end{aligned} \]
A height of \(-13.60m\) indicates that it is lower than where it begin. This means that it fell short of Elias and hit the ground.
Practice Your Parabolas!

You need to be able to solve all three types for the exam! We have covered Half and full parabolas so far, now we will do partial parabolas!.