Forces
12PHYS - AS91171
Finn Le Sueur
2024
Mahi Tuatahi
Draw a diagram indicating all the forces acting upon you
Drawing Force Diagrams
- Use these tips to draw a second, improved diagram
- Use arrows (force is a vector)
- Label with names
- Label with numerical values
- Start arrows from center of mass
- Length indicates magnitude
- Use dashes to indicate equally sized vectors

Muscle Contraction & Light-Headedness

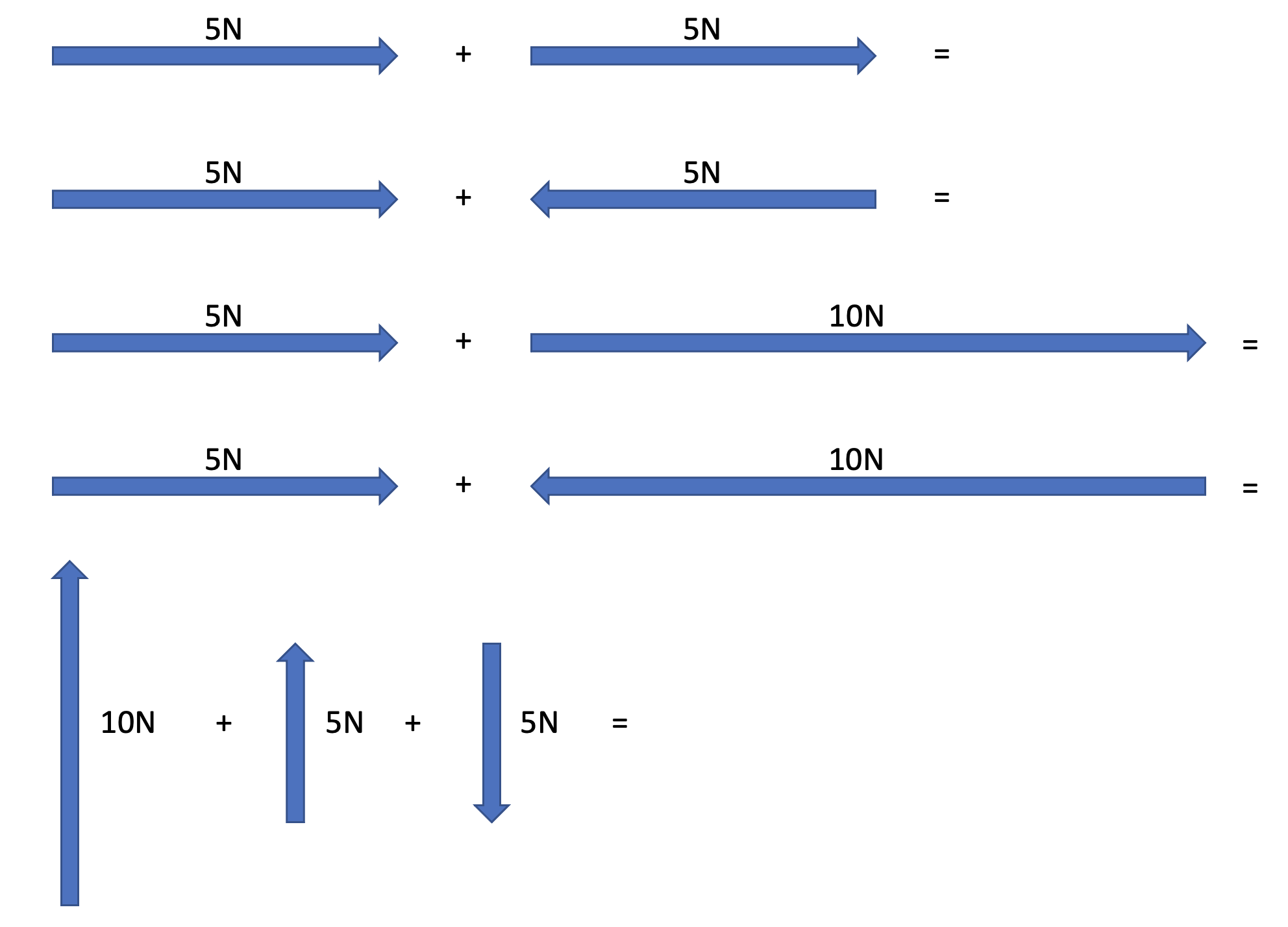
Pātai: Vector Reminder
- Draw a vector diagram for each situation.
- Illustrate and label the resultant force.
- Calculate the acceleration each experiences given \(m=5kg\).
Equilibrium
A state of zero acceleration (constant velocity) due to \(F_{net} = 0N\). E.g. vector diagram starts and ends at the same spot.
- Vector diagrams having different start and end points indicates disequilibrium, and thus \(F_{net} \neq 0N\).
Pātai: Terminal Velocity
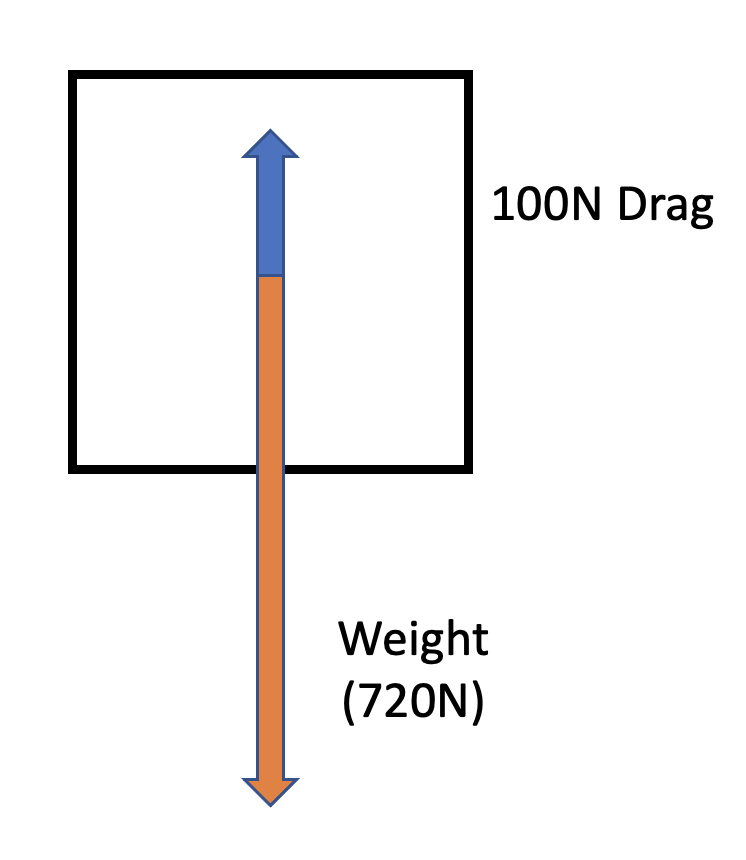
- What is my net force?
- What is my
acceleration?
- Why does it not equal \(g\)?
- What if my drag and weight forces were
balanced?
Whakatika

- What is my net force?
\(620N\) down - What is my acceleration?
\(F=ma, a=\frac{F}{m}=\frac{620}{72}=8.61ms^{-2}\) - Why does it not equal \(g\)?
Because friction is acting against the weight force! - What if my drag and weight forces were
balanced?
\(F_{net}=0\) and therefore \(a=0\) and I would be in equilibrium.
Akoranga 22 Mahi Tuatahi
Ngā Whāinga Ako
- Be able to label different forces
- Be able to label forces on an angle
Write the date and ngā whāinga ako in your book

- Friction: Acts against the direction of motion between two in-contact moving objects.
- Weight: Acts down towards the center of mass of the object attracting you.
- Applied: Often called thrust/push/pull depending on the situation.
- Drag: Acts against the direction of motion when an object moves through a medium (e.g. air)
- Spring: A compressed or extended spring can exert a force in the opposite direction to its displacement.
- Magnetic: A moving charged object inside an electric field will experience a magnetic force.
- Tension: A force exerted through a non-rigid object like rope
- Buoyant: A force felt due to the displacement of another medium (air, water)
- Normal/Support: A force exerted by a rigid object at \(90\degree\) to the surface (equal and opposite to the force being applied to it).
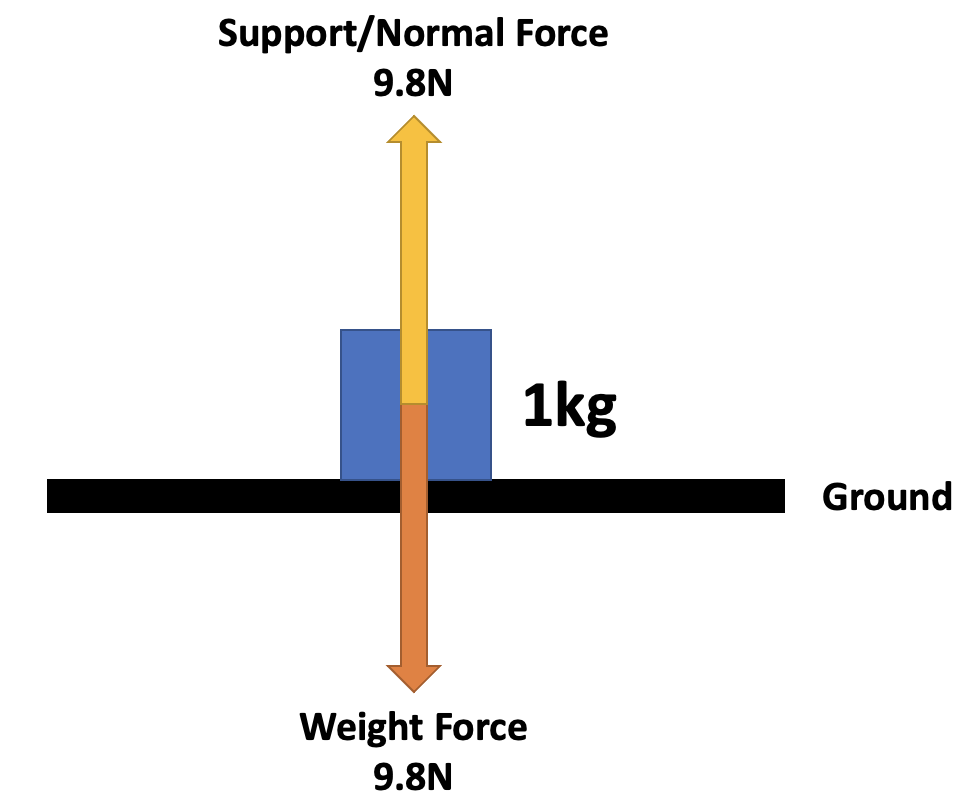
Support/Normal Force
- If the surface is sufficiently strong, the support/normal force will always oppose the force acting upon it exactly
- It will always act at \(90\degree\) to the surface
- ❗️ Draw equal and opposite weight and normal forces on your diagram.
- ❗️ What would occur if the support force was less than the weight force?
Whakatika
Support/Normal Forces on an Angle
- It will always act at \(90\degree\) to the surface
- In this case, the normal force does not equal the weight force
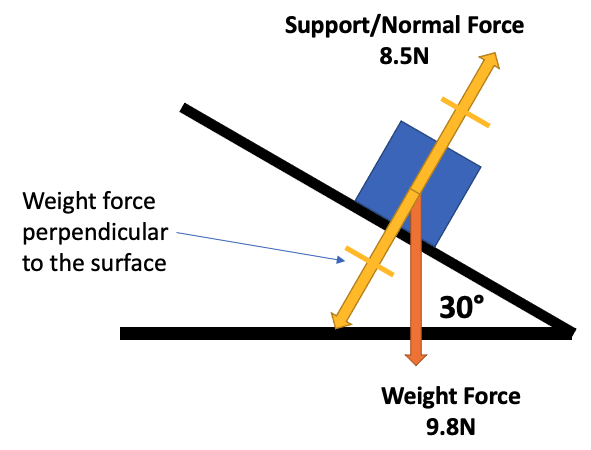
- This is because not all of the weight force is acting perpendicular to the surface.
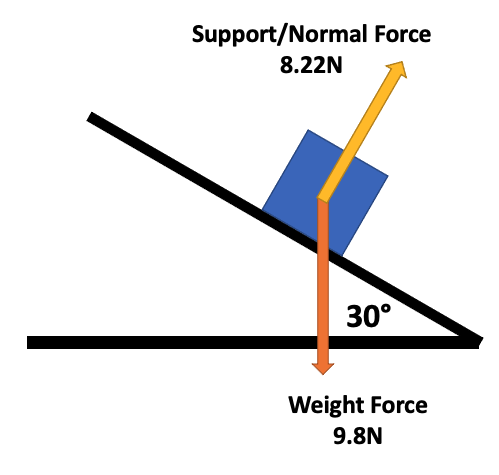
- Support is equal and opposite to the component of the weight force perpendicular to the surface.
- We can find it using the right triangle that is formed between the weight force exerted on the plane, and the total net force.
- \(F_{n} = F_{w}cos(\theta)\)
- The angle inside this triangle is the same as the angle of the incline.
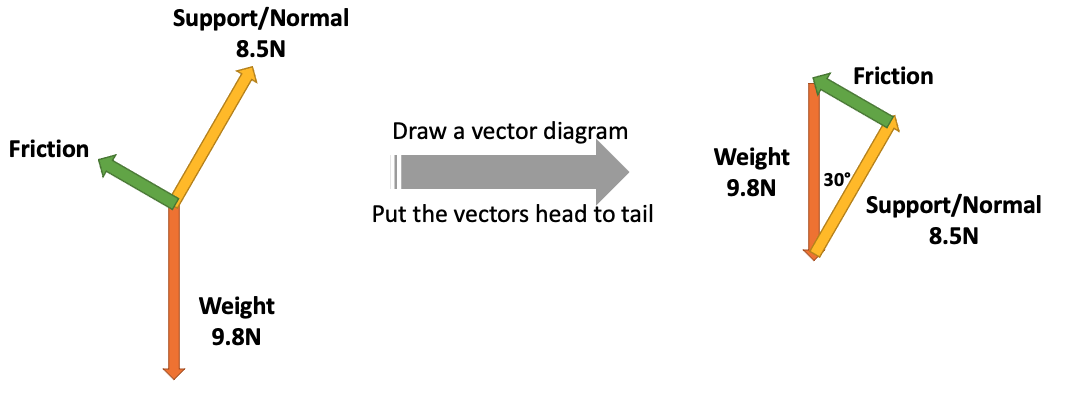
Calculating a Missing Force
- If an object is in equilibrium, we can calculate a missing force by knowing \(F_{net} = 0\) and drawing a vector diagram
- They should form a closed right-angled triangle, allowing you to find the unknown side with Pythag/trig.
Task/Ngohe
Worksheet - everything up to but not including the Work section.
Case Study

Step 1. Consider what we know about the motion of the object, and what this implies about the net force acting upon the object.
Question 1
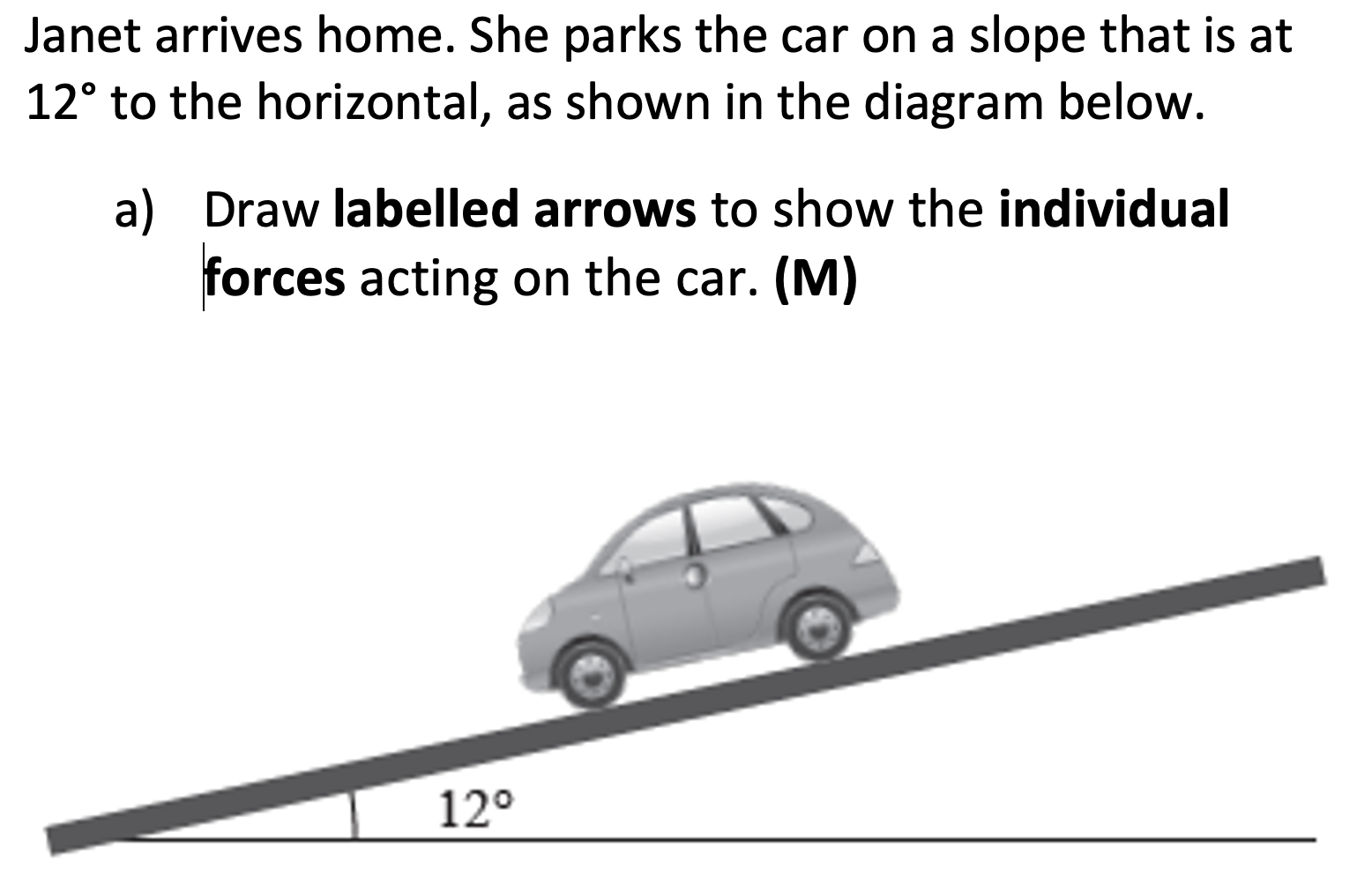
- What force do we know is not
acting due to the cars movement?
- Therefore, what three forces are
acting?
- Draw a force diagram illustrating these forces and their relative magnitude. Ensure you label them!
Question 1 Whakatika
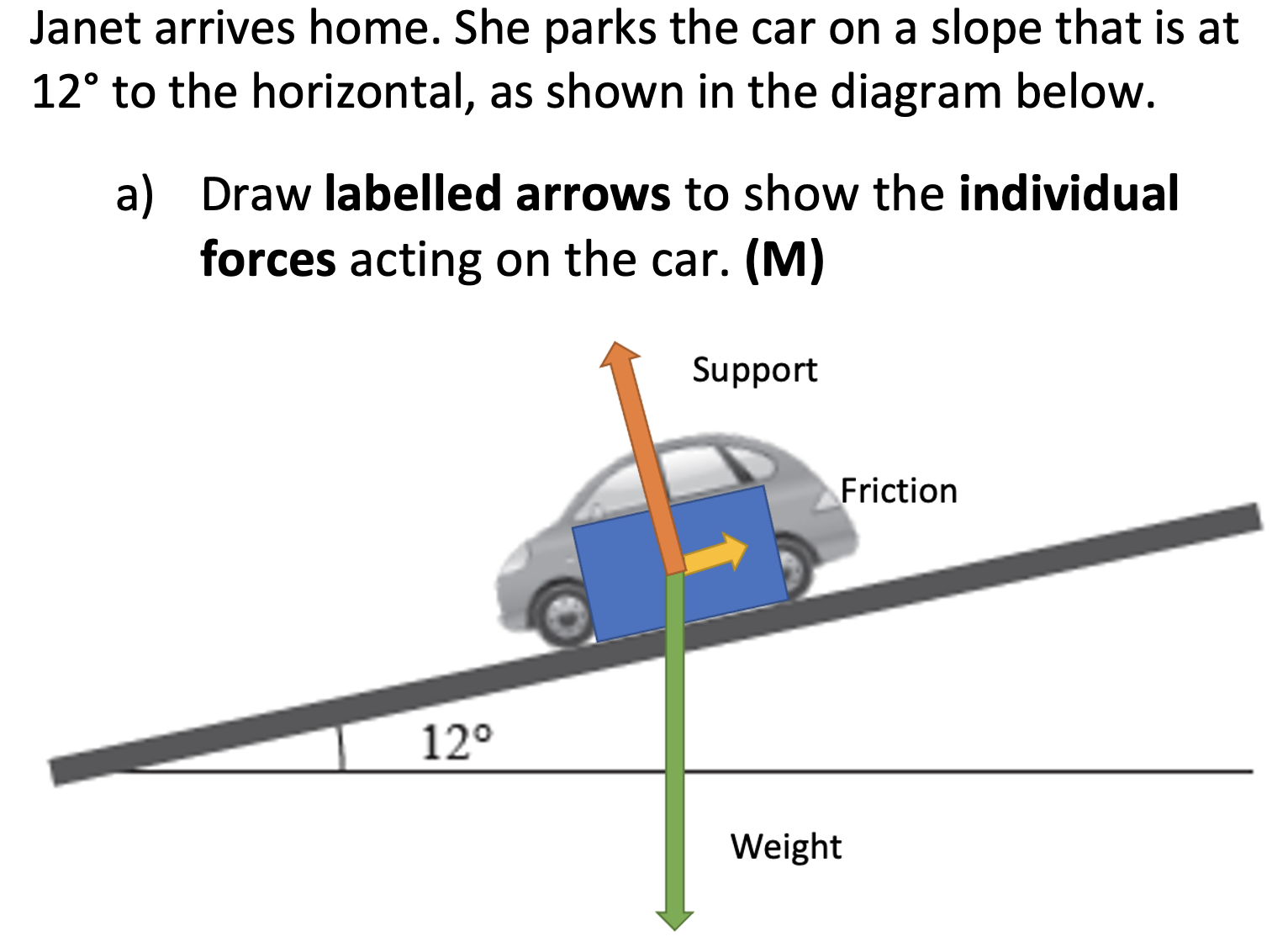
- What force do we know is not
acting due to the cars movement?
Thrust, because it is parked. - Therefore, what three forces are
acting?
Weight, friction and support. - Draw a force diagram illustrating these forces and their relative magnitude. Ensure you label them!
Question 2
- What do we know about the motion of the
car?
- Therefore, what can we say about its acceleration,
forces and state of equilibrium?
- Therefore, what do we know the vector diagram will
look like?
- Draw a diagram.
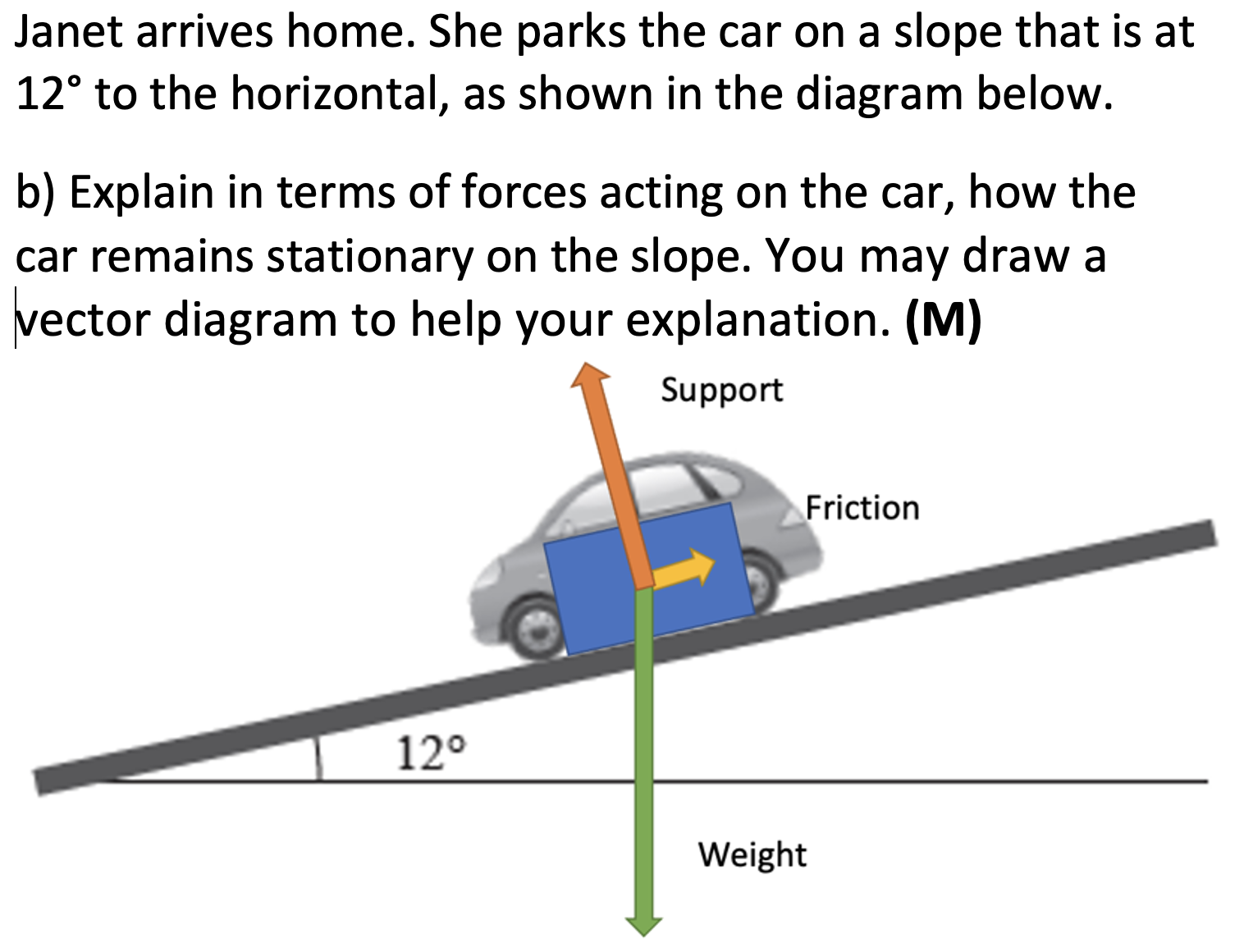
Question 2 Whakatika
- What do we know about the motion of the
car?
It is stationary (constant velocity). - Therefore, what can we say about its acceleration,
forces and state of equilibrium?
\(a=0, F_{net}=0\) and is therefore in equilibrium. - Therefore, what do we know the vector diagram will
look like?
The vectors will form a closed diagram. - Draw a diagram.
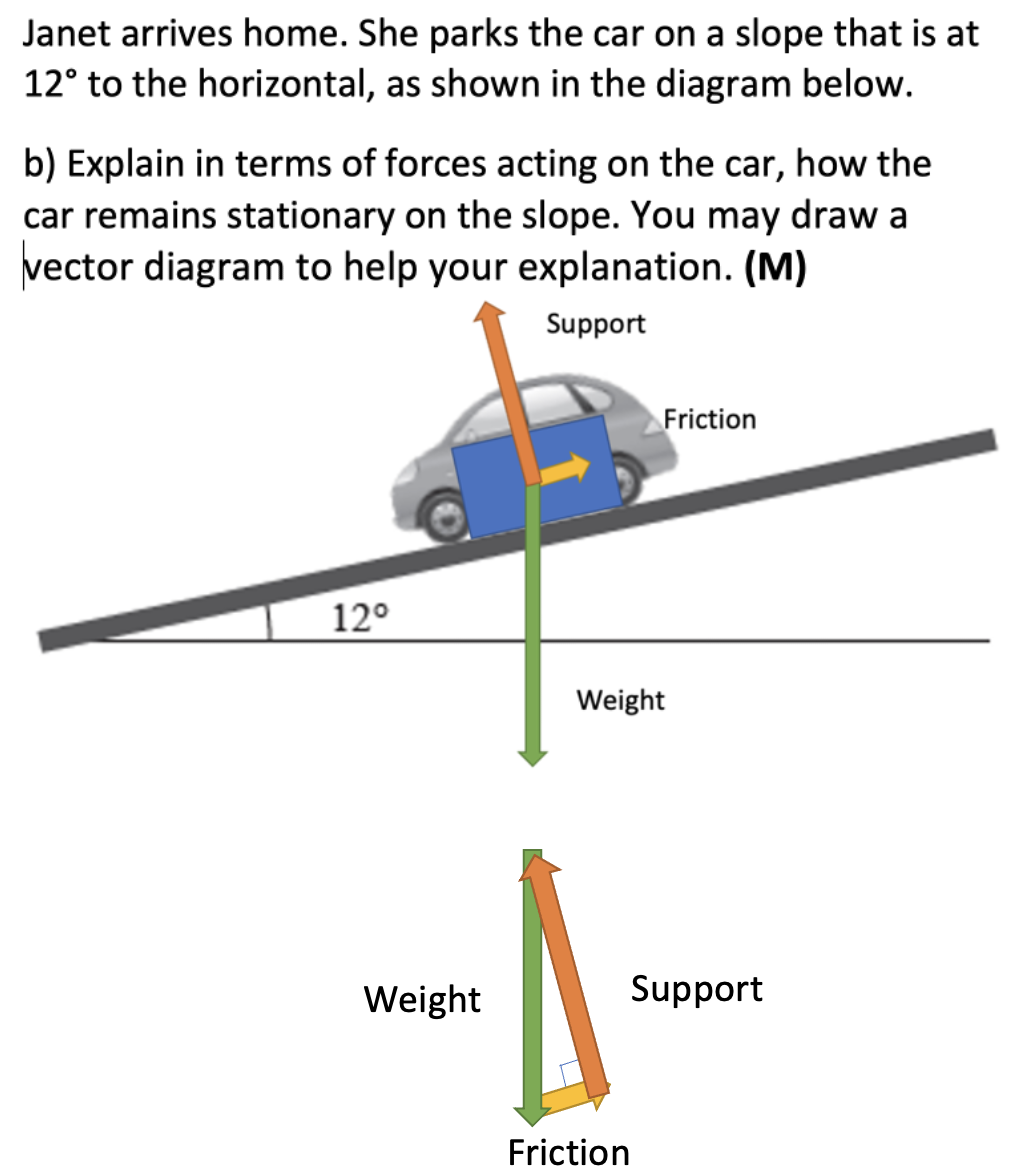
Question 3
- We need to calculate the weight
force of the car. Hint: \(F=ma\).
- Recognise & state that not all of the weight
force acts directly through the slope.
Question 3 Continued

- Recgonise and state we need to find component of
weight force acting into slope, and is equal in magnitude to the support
force. Hint: \(F_{n} =
F_{w}cos(\theta)\).
- Calculate \(F_{f}\) using EITHER Pythagoras OR trigonometry to find the frictional side of the triangle.
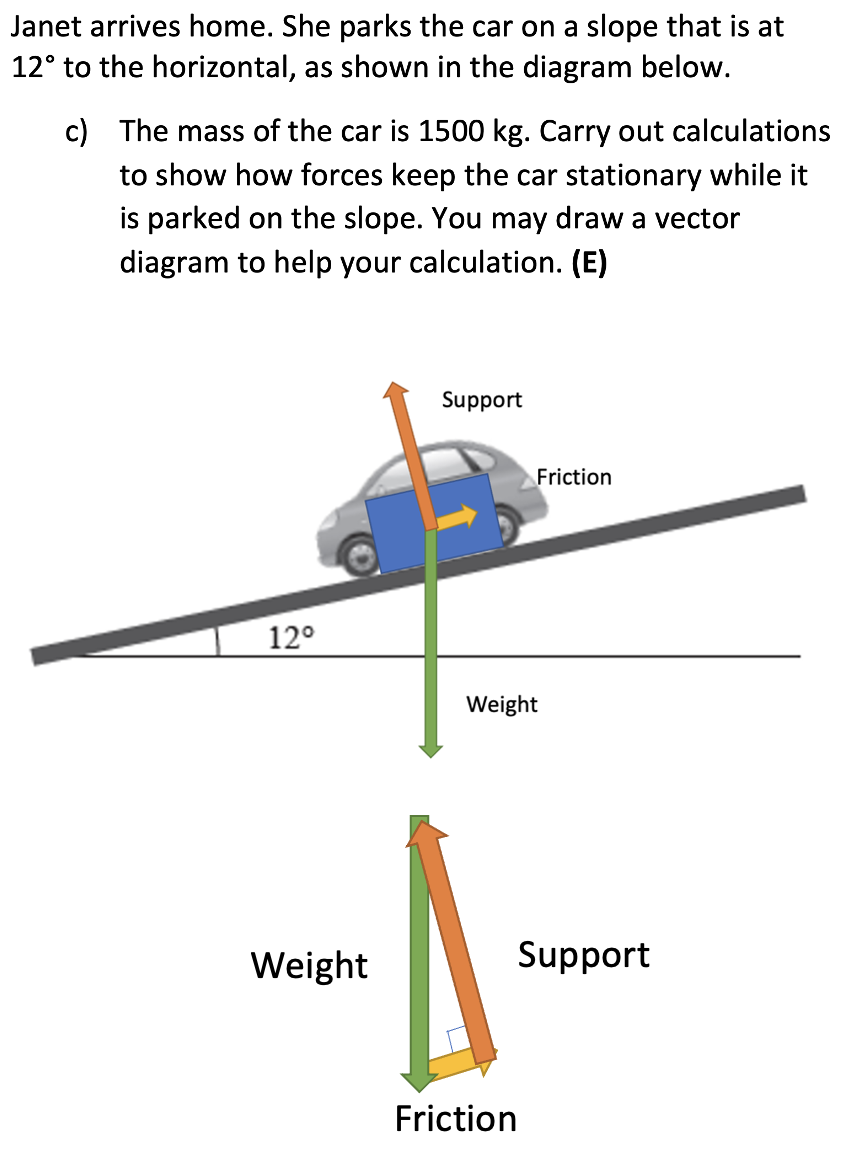
Question 3 Whakatika
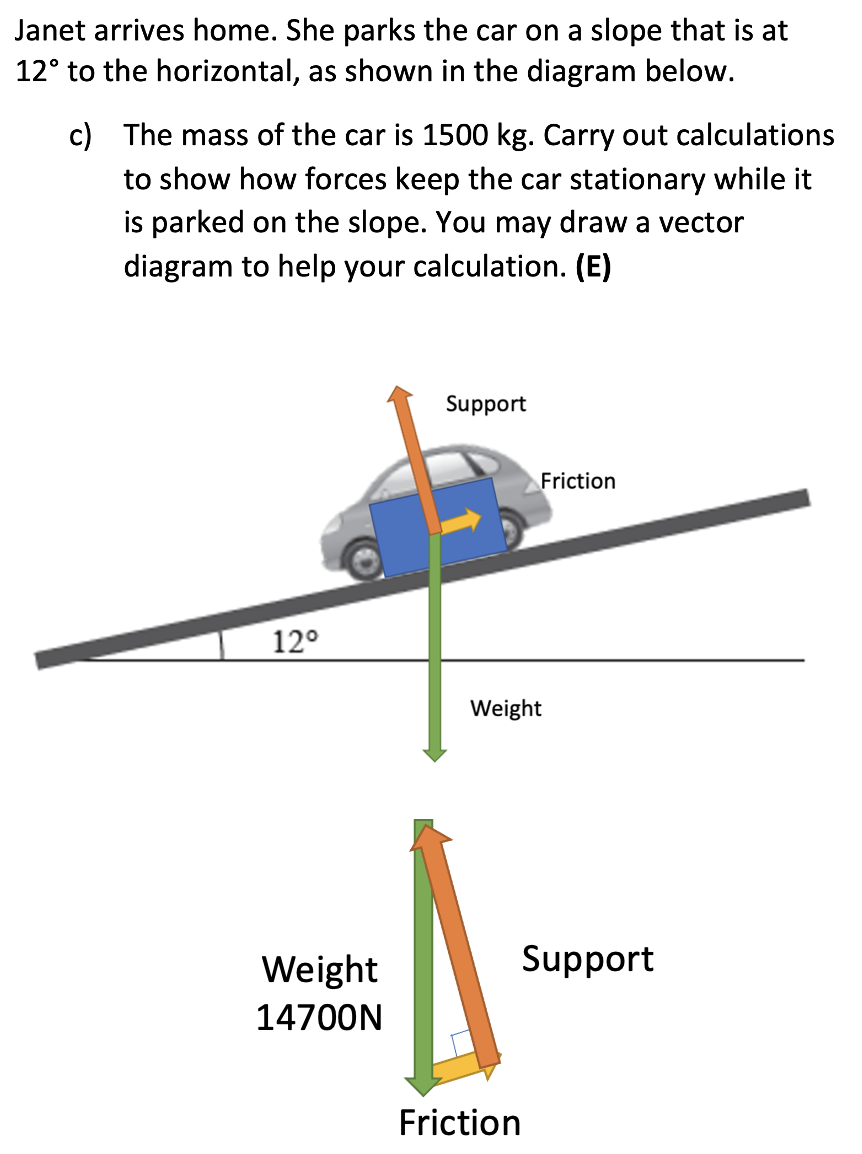
- We need to calculate the weight
force of the car. Hint: \(F=ma\).
\(W=F=m \times a = 1500 \times 9.8 = 14700N\). Use \(a = g\) because weight force is due to gravity. - Recognise & state that not all of the weight
force acts directly through the slope.
Because the weight force is acting on an angle to the slop, the component perpendicular to the slope is equal & opposite to the normal force.
Question 3 Whakatika Continued
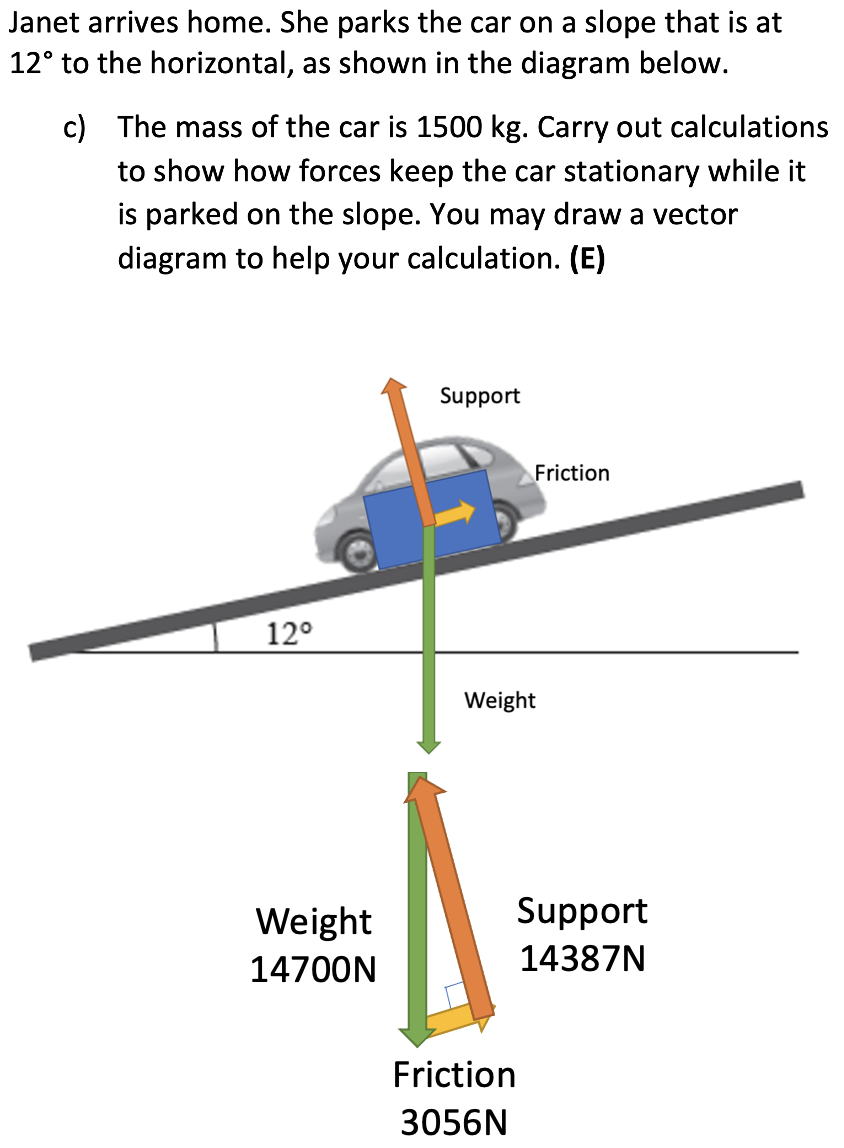
- Calculate the normal force. Hint: \(F_{n} = F_{w}cos(\theta)\).
\(F_{n} = 14700 cos(12) = 14378N\) - Calculate \(F_{f}\) using EITHER Pythagoras OR
trigonometry to find the frictional side of the triangle.
\(F_{f} = F_{w}sin(\theta) = 14700sin(12) = 3056N\)
OR
\(F_{f} = \sqrt{F_{w}^{2} - F_{n}^{2}} = 3056N\).
Practise / Whakawai
- Textbook
- New: Activity 10A: Newton’s Laws
- Old: Activity 9A: Newton’s Laws
- Homework Booklet: Q31, Q32, Q34