Circular Motion
12PHY - Mechanics
Finn Le Sueur
2024
Mahi Tuatahi
Aaron is painting the outside of his house. He is standing on a \(3.5m\) long plank with a support at each end. The plank weighs \(4.8kg\). He is standing \(0.8m\) from the left side and he weighs \(63kg\).
- Draw a diagram to illustrate the situation
- Calculate the support force provided by Support A (left) and Support B (right).
Circular Motion
The motion of an object moving in a circular path.
e.g. Satellites in orbit, car driving around a corner, discus thrower, cricket bowler.
Circles
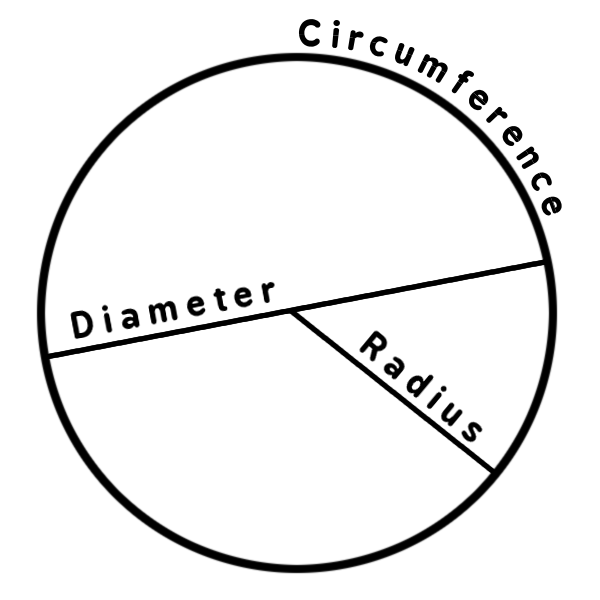
\[ \begin{aligned} & Radius = r \cr & Diameter = d \cr & Circumference = C \end{aligned} \]
Pātai Tahi (Q1): Circumference
- How do we calculate circumference?
- Whakatika: \(C = 2\pi r\)
- Where \(r\) is the radius of the circle

Pātai Rua (Q2): What is Frequency?
- Frequency is the number of rotations in one second.
- It is given the symbol \(f\) and measured in \(s^{-1}\) (per second).
Pātai Toru (Q3): What is Period?

- Period is the time taken to do one revolution.
- It is given the symbol \(T\) and is measured in \(s\) (seconds).
- Period and frequency are inversely related via this equation
- \(T = \frac{1}{f}\)
Pātai

- Measure the period (\(T\))
- Calculate the frequency (\(f\))
Velocity on a Circle

- Velocity is always given by \(v = \frac{d}{t}\)
- On a circle, \(d = C = 2 \pi r\)
- On a circle, \(t = T = \frac{1}{f}\)
- Therefore, circular velocity is \(v = \frac{2\pi r}{T}\)
Pātai Whā (Q4): Finding Velocity

- If the radius is 2m, find the: circumference,
- and speed
Whakatika

- If the radius is 2m, find the:
circumference,
- \(C = 2 \pi r = 2 \pi 2 = 12.57m\)
- period,
- \(T = 12s\)
- frequency
- \(f = \frac{1}{T} = \frac{1}{12} = 0.083^{-s}\)
- and speed
- \(v = \frac{d}{t} = \frac{12.57}{12} = 1.0475ms^{-1}\)
Pātai Rimu (Q5)

- Is speed constant? Explain.
- Is velocity constant? Explain.
Whakatika

- Is speed constant?
- Speed is constant, because the magnitude of the velocity is constant.
- Is velocity constant?
- Velocity is not constant, because even though the magnitude is constant, the direction is changing.
Centripetal Acceleration
An object undergoing circular motion is always accelerating towards the center of the circle. Therefore, because the direction is changing, the velocity is changing. Therefore the object is always accelerating, even if its speed is constant.
\[ \begin{aligned} a_{c} &= \frac{v^{2}}{r} \end{aligned} \]
Mahi Tuatahi
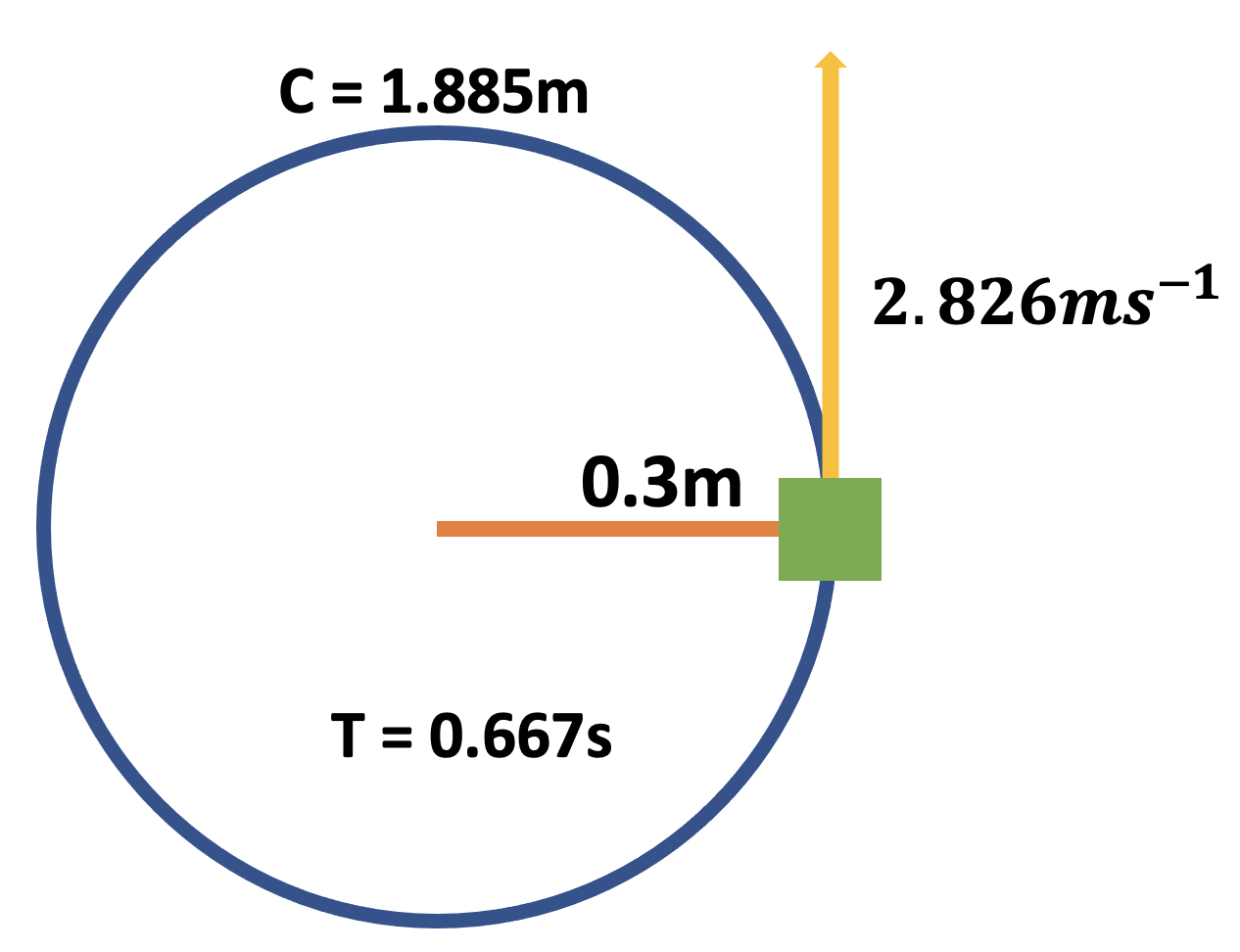
- An ice skater performs a 720 degree jump. The outside of their shoulders rotate with a frequency of \(1.5s^{-1}\). Calculate the period of their rotations.
- If their shoulders are \(30cm\) from their center of rotation, calculate their linear velocity.
- Draw a diagram illustrating the things you know about their circle of rotation.
Whakatika
- An ice skater performs a 720 degree jump.
The outside of their shoulders rotate with a frequency of \(1.5s^{-1}\). Calculate the period of their
rotations.
\(T = \frac{1}{f} = \frac{1}{1.5} = 0.667s\) - If their shoulders are \(30cm\) from their center of rotation,
calculate their linear velocity.
\(v=\frac{2 \pi r}{T} = \frac{2 \pi 0.3}{0.667} = 2.826ms^{-1}\) - Draw a diagram illustrating the things you know about their circle of rotation.
What Causes the Acceleration?
- Newton 2nd Law tells us via \(F=ma\) that an acceleration is caused by an unbalanced force.
- Therefore, centripetal (center-seeking) acceleration is caused by an unbalanced force which continuously pulls the object towards the center. Centripetal force.
- Net force and acceleration are always in the same direction.

Centripetal Force
\[ \begin{aligned} & F_{c} = \frac{mv^{2}}{r} \end{aligned} \]
- Centripetal force \(\rightarrow\) centripetal acceleration \(\rightarrow\) change direction of velocity \(\rightarrow\) move in a circular path.
- Therefore, if the centripetal force is removed, the object will move in a straight line tangent to the circle.
Pātai Ono (Q6): Bucket of Water
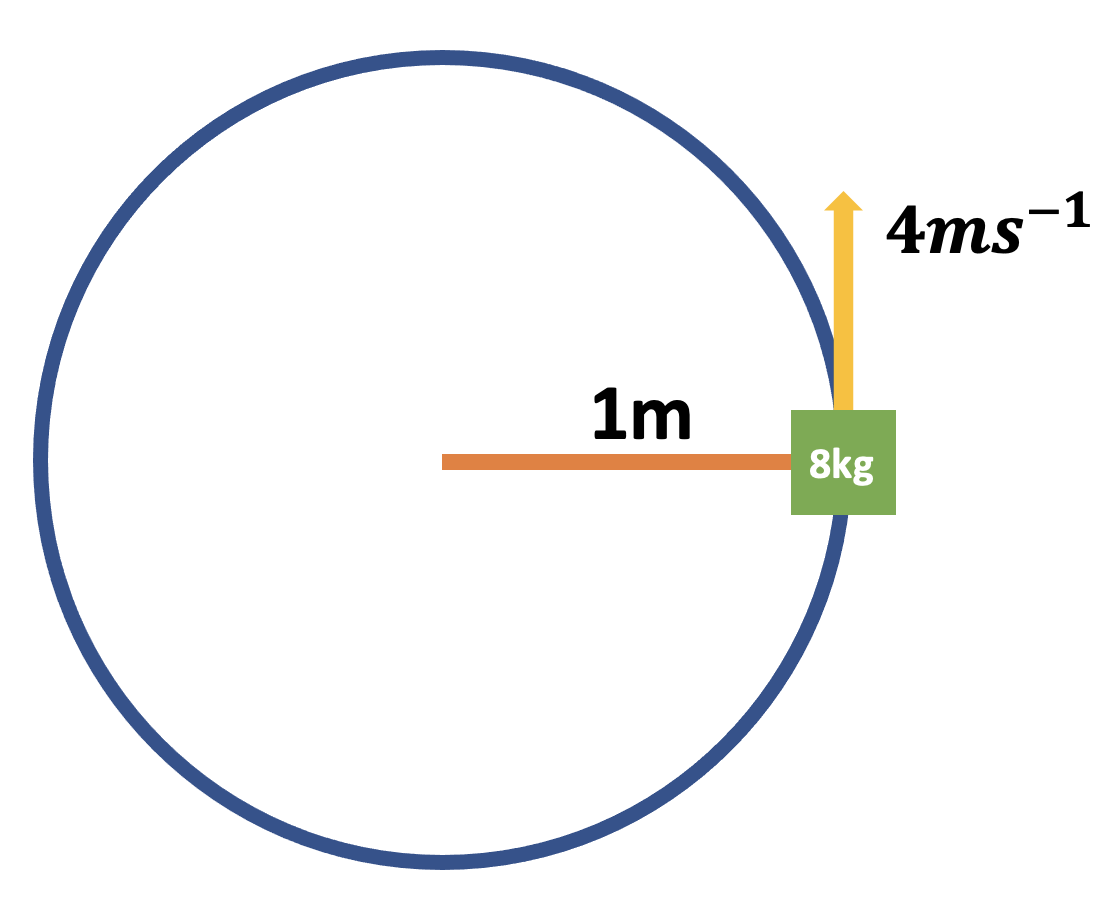
- Mathieu is swinging a bucket of water above his head. It weighs, \(8kg\) and has a horizontal speed of \(4ms^{-1}\) in a circle of radius \(1m\).
- Calculate the force required to keep the
bucket moving in a circle.
- Knowns, Unknowns, Formula, Substitute, Solve
Whakatika

\[ \begin{aligned} & v = 4ms^{-1}, r = 1m, m = 8kg && \text{(K)} \cr & F_{c} = ? && \text{(U)} \cr & F_{c} = \frac{mv^{2}}{r} && \text{(F)} \cr & F_{c} = \frac{8 \times 4^{2}}{1} = 128N \text{ inwards} && \text{(S+S)} \end{aligned} \]
NB: From 2:30 to 5:25.
Pātai Whitu (Q7): Hammer Throw
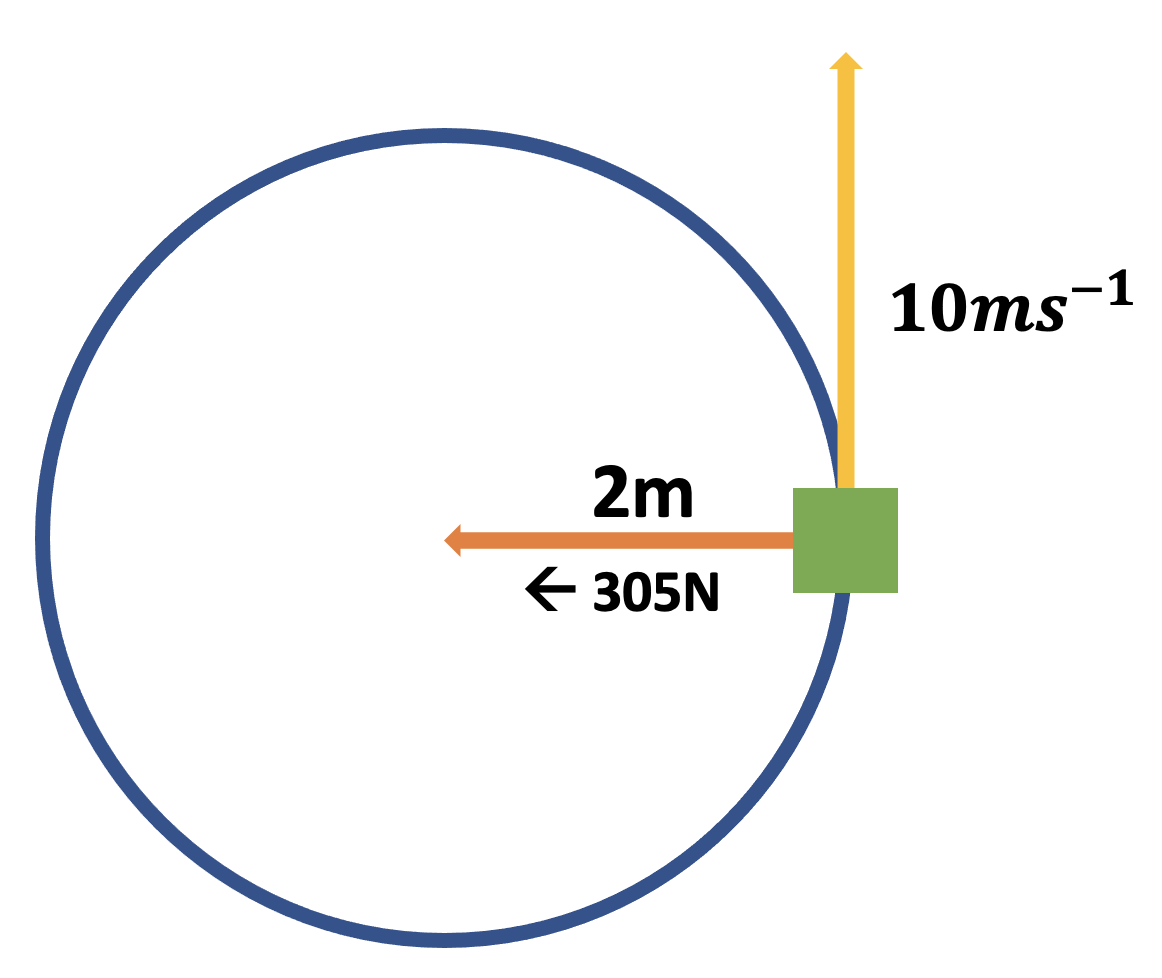
- During a hammer throw, a steel ball is swung horizontally with a speed of \(10ms^{-1}\) in a circle of radius \(2m\). \(350N\) of tension force is required.
- Calculate the mass of the steel
ball.
- Knowns, Unknowns, Formula, Substitute, Solve
Whakatika
\[ \begin{aligned} & F_{c} = 350N, v = 10ms^{-1}, r = 2m && \text{(K)} \cr & m = ? && \text{(U)} \cr & F_{c} = \frac{mv^{2}}{r} && \text{(F)} \cr & 350 = \frac{m \times 10^{2}}{2} && \text{(S+S)} \cr & \frac{350 \times 2}{10^{2}} = m = 7kg \end{aligned} \]
Whakawai / Practice
- Homework Booklet Q26
- Mahi kainga (homework): Q28 due April 4th