Newton’s First Law ^🔗

Every object persists in its state of rest or uniform motion in a straight line unless it is compelled to change that state by forces impressed on it.

TLDR: A non-zero net force will induce a change in velocity (an acceleration).

Examples ^🔗

• Car Crash: A person not wearing a seatbelt during a crash will continue their motion forwards as the car suddenly stops.
• Ball: A ball rolling on a soccer field will come to a stop because of the friction force acting upon it, creating a negative acceleration (deacceleration).

Newton’s Second Law ^🔗

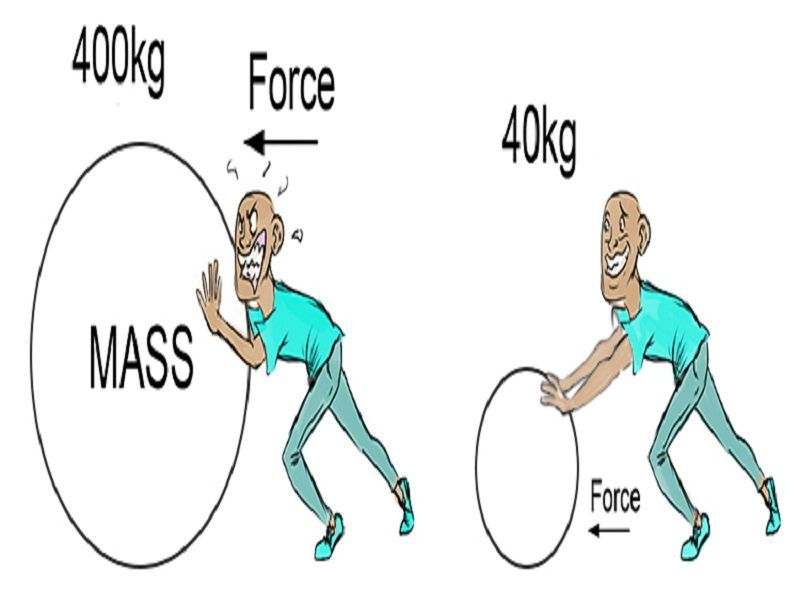
Force is equal to the change in momentum per change in time. For a constant mass, force equals mass times acceleration. $F=m \times a$

TLDR: The acceleration created by a force depends directly upon the mass of the object.

Examples ^🔗

• A student pushing a trolley can cause a great deal of acceleration
• A student pushing a car will cause very little (or no acceleration)

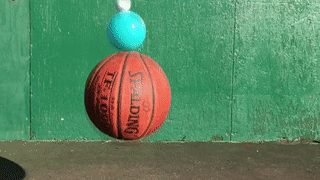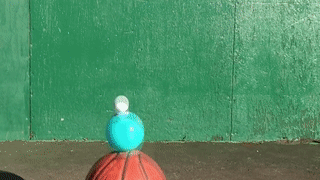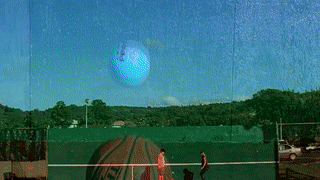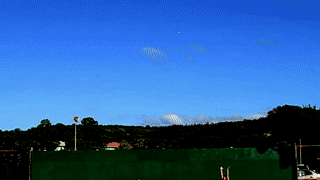
Newton’s Third Law ^🔗

For every action, there is an equal and opposite reaction.

Examples ^🔗

• Rockets: Gas is ignited causing it to heat and expand. It is expelled out a narrow nozzel at a high velocity. An equal and opposite force is exerted on the spacecraft causing it to move forwards.
• Bouncing Balls: A ball thrown on the ground exerts a force on contact. The ground exerts an equal and opposite force which causes the ball to bounce.

Pātai ^🔗

With the person next to you, write a paragraph describing how Newton’s 1st and 2nd Laws relate to projectile motion.

Whakatika ^🔗

• Newton’s 1st Law
  • A non-zero net force will induce a change in velocity (an acceleration)
  • In the x-direction there are no forces acting (friction is negligible).
  • In the y-direction there is only the weight force of the object. This means the resultant force is in the downwards direction.
  • An constant acceleration is therefore induced in the downwards direction at all times.

• Newton’s 2nd Law
  • The acceleration created by a force depends directly upon the mass of the object.
  • In Earth’s gravitational field at sea level, $g=9.81ms^{-2}$ at all times, and therefore the object is accelerated uniformly down.

Whakawai/Practise ^🔗

• Try Q1-3 of Activity 10A: Using Newton’s Laws in your textbook.
• Draw a diagram each time!