Speed-Time Graphs
11SCI - Mechanics
Finn Le Sueur
2024
Mahi Tuatahi

Calculate and describe the velocity in each section of this distance-time graph. Time is in minutes.
Speed-Time Graphs
- The gradient of a distance-time graph is the velocity
- The gradient of a speed-time graph is the acceleration
- The area under a speed-time graph is the distance travelled
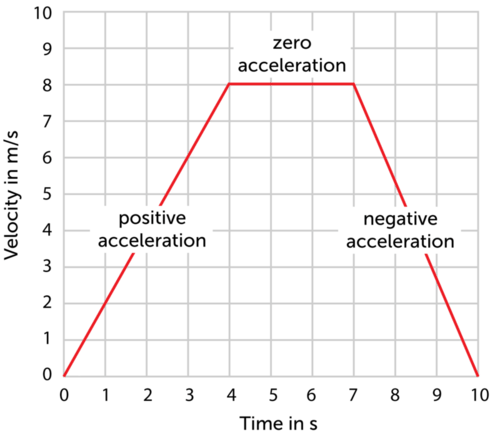
Calculating Acceleration

\[ \begin{aligned} a &= \frac{rise}{run} \cr a &= \frac{\Delta v}{\Delta t} \cr a &= \frac{v_{f} - v_{i}}{t_{f} - t_{i}} \end{aligned} \]
Pātai

- Calculate the acceleration for the positive acceleration section
- Show, with maths, the acceleration is zero for the middle section
- Calculate the acceleration for the negative acceleration section
Finding the Distance

- Calculate the area under the speed-time graph to find the distance travelled
- Break it up into rectangles & triangles to calculate the area
- Finding area of a rectangle is \(A = B \times H\)
- On the graph \(d = t \times v\)
- This should look familiar from \(v=\frac{d}{t} \rightarrow d = v \times t\)!
Pātai
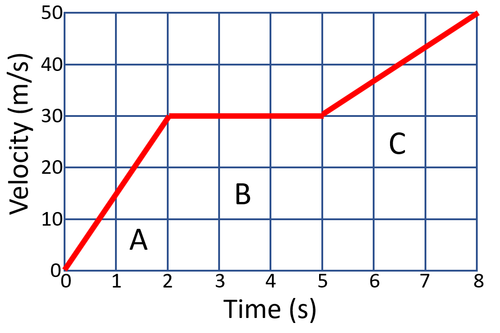
- Find the distance travelled in sections A, B and C
- Find the total distance travelled
- Describe the acceleration in each of A, B and C
- Describe the velocity in each of A, B and C
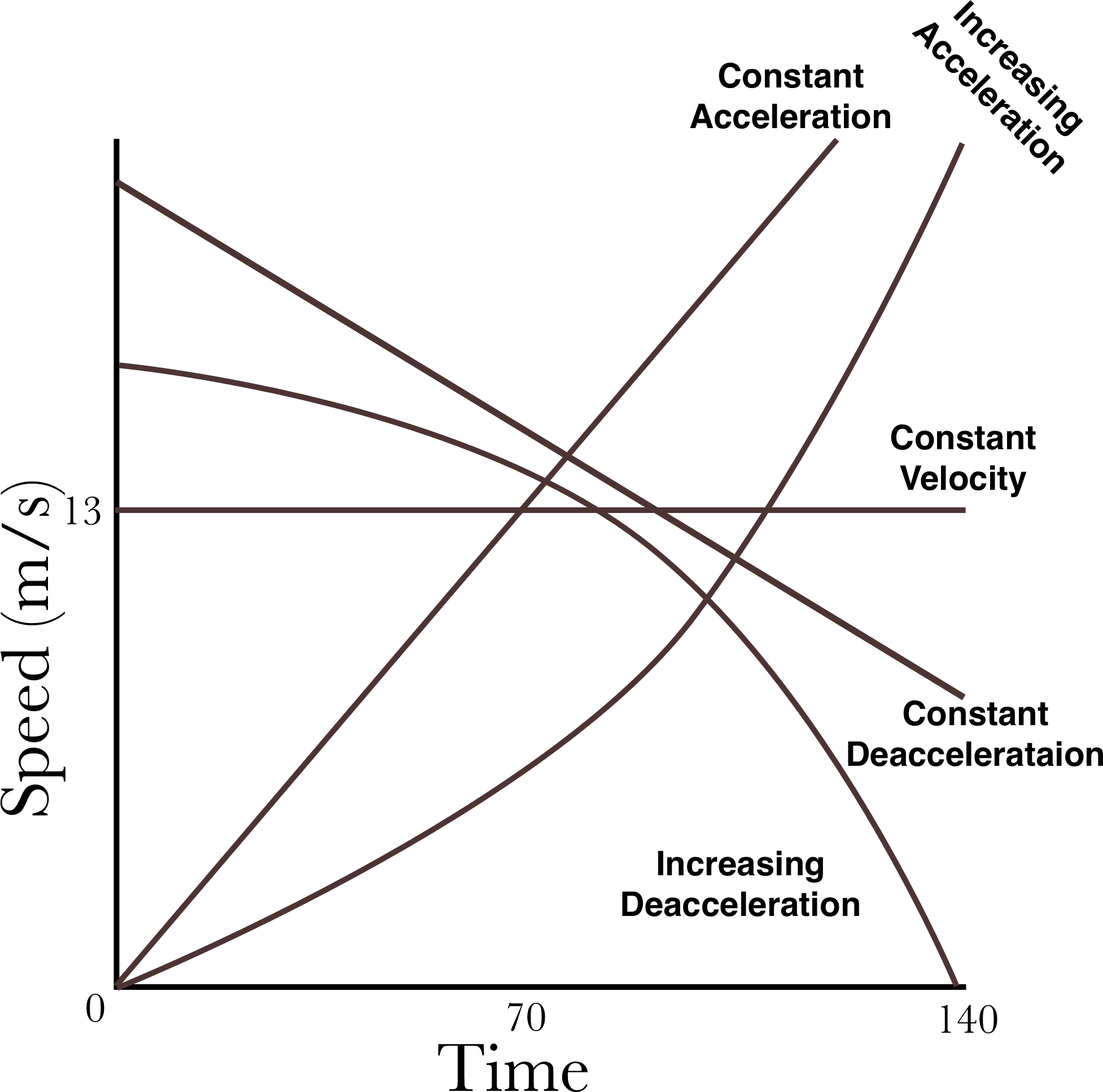
Questions
sciPAD Pages 18-21