Pressure

Ngā Whāinga Ako

Copy these learning outcomes and the date into your books!

1. Recap forces
2. Explain force and pressure in terms of everyday situations. Use \(P = F/A\).

Mahi Tuatahi

1. Calculate the net force acting upon these objects:

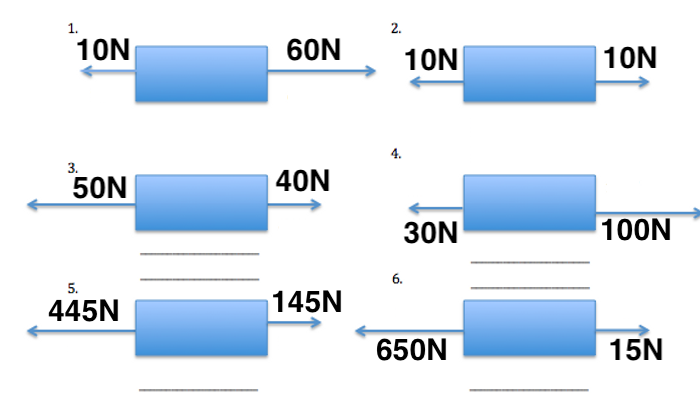
2. What does an unbalanced force do to the motion of an object?

Whakatika Rua

It causes the object to accelerate (or de-accelerate).

We know this because of the equation

\[ \begin{aligned} force &= mass\times acceleration \cr F &= m \times a \end{aligned} \]

Pātai Toru

For the followig equation give the name and unit for each variable in the equation.

\[ \begin{aligned} & F = m \times a \end{aligned} \]

Whakatika Toru

• F stands for force and has units Newtons (N)
• m stands for mass and has units kilograms (kg)
• a stands for acceleration and has units meters per second squared (\(ms^{-2}\))

Pātai Whā

• What do you think of when you think of pressure?
• What affects the pressure exerted by an object?

Pātai Rima

The most classic case of pressure is sharpening a knife. Why do we sharpen knives? What does sharpening a knife change about the knife?

Pressure / Pēhanga

The amount of force per square meter

\[ \begin{aligned} pressure &= \frac{force}{area} \cr P &= \frac{F}{A} \end{aligned} \]

• Force (F) is measured in Newtons (N)
• Area (A) is measured in meters squared (\(m^{2}\))

\[ \begin{aligned} P &= \frac{F}{A} \cr P &= \frac{Newtons}{m^{2}} \end{aligned} \]

• Therefore, pressure is measured in Newtons per meters squared (\(\frac{N}{m^{2}}\) OR \(Nm^{-2}\))
• This is also known as a Pascal (Pa): \(Pa = \frac{N}{m^{2}} = Nm^{-2}\)
• You may use whichever unit you prefer.

Calculating Pressure

\[ \begin{aligned} P = \frac{F}{A} \end{aligned} \]

1. Calculate the pressure created by a force of \(3N\) with an area of \(0.5m^{2}\)
2. Calculate the area used by a force of \(3N\) with pressure \(7Pa\)
3. Calculate the force created by a pressure of \(5Nm^{-2}\) with an area of \(0.125m^{2}\)

Whakatika Tahi

\[ \begin{aligned} F&=3N, A=0.5m^{-2}, P=? \cr P &= \frac{F}{A} \cr P &= \frac{3}{0.5} \cr P &= 6Nm^{-2} = 6Pa \end{aligned} \]

Whakatika Rua

\[ \begin{aligned} F&=3N, P=7Pa, A=? \cr P &= \frac{F}{A} \cr A &= \frac{F}{P} \cr A &= \frac{3}{7} \cr A &= 0.43m^{-2} \end{aligned} \]

Whakatika Toru

\[ \begin{aligned} P&=5Nm^{-2}, A=0.125m^{-2}, F=? \cr P &= \frac{F}{A} \cr F &= PA \cr F &= 5 \times 0.125 \cr F &= 0.625N \end{aligned} \]

Pressure Whakamātau

Open Google Classroom and find the Pressure Whakamātau document.

Mahi Tuatahi (2018 Exam)

Jacob bikes down The Flying Nun. He and his bike have a mass of \(82kg\) and he accelerates at \(0.8ms^{-2}\).

1. Calculate the net force acting upon Jacob and his bike to cause this acceleration
2. Draw a force diagram showing the forces acting upon Jacob as he accelerates
3. Describe the size and direction of the forces compared to each other (horizontal and vertical)

Exam Question (2018)

Giovanni is running a 100m sprint. Each of his feet have a surface area of \(200cm^{2}\) (\(0.0200m^{2}\)), which sink into the track. Together, his feet exert a pressure of \(13000Pa\). Calculate Giovanni’s weight.

Whakatika

Because weight is a force, we know that we are looking for \(F\).

\[ \begin{aligned} P &= 13000Pa \cr A &= 0.02m^{2} \times 2 = 0.04m^{2} \cr F &= P \times A \cr F &= 13000 \times 0.04 \cr F &= 520N \end{aligned} \]