Te Whāinga Ako ^🔗

1. Describe how resistance controls the flow of electric current

Write the date and te whāinga ako in your book

Resistance ^🔗

• Resistance is a measure of how difficult it is for charges (electrons) to flow through a circuit component
• A higher resistance ➡ lower current
• A lower resistance ➡ higher current
• It is letter $R$ in equations
• It has the unit Ohm, given the Greek letter capital Omega: $\Omega$

^🔗

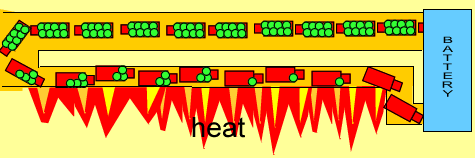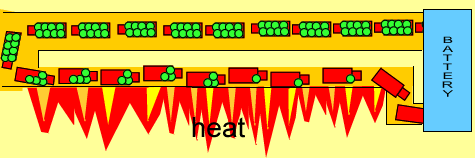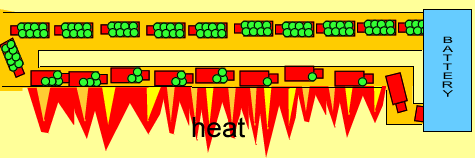
• You can think of it as a skinny pipe which cannot carry as much water as a larger pipe
• When electrons move through a material with resistance, they lose some energy in the form of heat (and light, when hot enough)
• E.g. your toaster, filament lightbulbs, hair dryer, heater, hair straightener
• Materials with very high resistance are called insulators
• Materials with very low resistance are called conductors

The amount of resistance in a component is related directly to the voltage and current flowing through it. This equation is known as Ohm’s Law.

\begin{aligned} &V &&= &&&I &&&&\times &&&&&R \newline &\downarrow && &&&\downarrow &&&& &&&&&\downarrow \newline &voltage &&= &&&current &&&&\times &&&&&resistance \newline &\downarrow && &&&\downarrow &&&& &&&&&\downarrow \newline &volts &&= &&&amperes &&&&\times &&&&&ohms \newline &\downarrow && &&&\downarrow &&&& &&&&&\downarrow \newline &V && &&&A &&&& &&&&&\Omega \end{aligned}

Pātai Tahi ^🔗

An current of $1A$ flows through a resistor with resistance $2\Omega$. Calculate the voltage consumed by the resistor.

\begin{aligned} &\text{(Knowns)} \newline &\text{(Unknowns)} \newline &\text{(Formula)} \newline &\text{(Substitute + Solve)} \end{aligned}

Whakatika ^🔗

\begin{aligned} & I = 1A, R = 2\Omega && \text{(K)} \newline & V = ? && \text{(U)} \newline & V = IR && \text{(F)} \newline & V = 1 \times 2 = 2V && \text{(S+S)} \end{aligned}

Pātai Rua ^🔗

An current of $0.01A$ flows through a resistor with resistance $1000\Omega$. Calculate the voltage consumed by the resistor.

\begin{aligned} &\text{(Knowns)} \newline &\text{(Unknowns)} \newline &\text{(Formula)} \newline &\text{(Substitute + Solve)} \end{aligned}

Whakatika ^🔗

\begin{aligned} & I = 0.01A, R = 1000\Omega &&\text{(K)} \newline & V = ? &&\text{(U)} \newline & V = IR &&\text{(F)} \newline & V = 0.01 \times 1000 = 10V &&\text{(S+S)} \end{aligned}

Pātai Toru ^🔗

An current of $0.01A$ flows through a resistor with resistance $50000\Omega$. Calculate the voltage consumed by the resistor.

\begin{aligned} &\text{(Knowns)} \newline &\text{(Unknowns)} \newline &\text{(Formula)} \newline &\text{(Substitute + Solve)} \end{aligned}

Whakatika ^🔗

\begin{aligned} & I = 0.01A, R = 50000\Omega && \text{(K)} \newline & V = ? && \text{(U)} \newline & V = IR && \text{(F)} \newline & V = 0.01 \times 50000 = 5000V && \text{(S+S)} \end{aligned}

Pātai Whā ^🔗

An current of $0.01A$ flows through a $6V$ bulb. Calculate the resistance of the bulb.

\begin{aligned} &\text{(Knowns)} \newline &\text{(Unknowns)} \newline &\text{(Formula)} \newline &\text{(Substitute + Solve)} \end{aligned}

Whakatika ^🔗

\begin{aligned} & I = 0.01A, V = 6V && \text{(K)} \newline & R = ? && \text{(U)} \newline & V = IR && \text{(F)} \newline & 6 = 0.01 \times R \text{(S+S)} \newline & \frac{6}{0.01} = R = 600\Omega \end{aligned}

Pātai Rimu ^🔗

Calculate the current that flows through a $10V$ bulb with a resistance of $400\Omega$.

\begin{aligned} &\text{(Knowns)} \newline &\text{(Unknowns)} \newline &\text{(Formula)} \newline &\text{(Substitute + Solve)} \end{aligned}

Whakatika ^🔗

\begin{aligned} & V = 10V, R = 400\Omega && \text{(K)} \newline & I = ? && \text{(U)} \newline & V = IR && \text{(F)} \newline & 10 = I \times 400 && \text{(S+S)} \newline & \frac{10}{400} = I = 0.025A \end{aligned}

Tūhura/Investigation: Ohm’s Law ^🔗

1. Open the PhET Simulation on Google Classroom.
2. The voltage and resistance sliders allow you to change those properties of the circuit.
3. What impact does increasing the voltage have on the circuit? Extra: Why?
4. What impact does increasing the resistance have on the circuit? Extra: Why?

Whakatika ^🔗

1. What impact does increasing the voltage have on the circuit? Extra: Why?
   Increasing the voltage increases the current in the circuit. Because a higher “pressure” is exerted by the power source, causing more electrons to flow around the circuit.
2. What impact does increasing the resistance have on the circuit? Extra: Why?
   Increasing the resistance decreases the current in the circuit. Because there is more friction acting upon the electrons, stopping them from flowing as freely.